بسم الله الرحمن الرحیم
بسم الله الرحمن الرحیم
[1]ما از حیث موطنهایی که در آن، قوای درک داریم:
یک مشاعر[2] داریم و یک عقل. مقصودمان از این واژهها را در ادامه روشن میکنیم.مشاعرِ ما، یک سنخی از قوای مدرکه هستند، یک حوزهای از مدرکات هستند؛ عقل ما هم یک سنخی و یک حوزهای، هر کدام از این ها هم مراتبی دارد.[3]
مشاعر ما کلاً سروکارش با فرد است؛ با وجود است. هر موجود فردی از طبیعت است. فرد الطبیعی را معمولاً همه میشناسند. مشاعر ما، سروکارش با افراد است،
اما عقل، سروکارش با طبایع است. بهطور کلی هر کجا سروکار شما با فرد است، ریختش، ریخت فرد است؛ نه ریخت طبیعی، این را ما میگوییم مشاعر.
مشاعر ما دو تا حیطه مهم دارد:
قیدِ مثال، این است که ماده به معنای هیولی ندارد اما آثار ماده را دارد .گفتند: مثال متصل یعنی قوّهی خیال؛صُوَر علمیّهای که بند به نفس ماست.
مثال منفصل یعنی چه؟ یعنی صوری است ملکوتیه که بند به کسی نیست و مجرّد است؛لذا گفتند مثال است، یعنی مادی نیست، اما منفصل است؛ یعنی بند به ذهن کسی نیست.
این اصطلاح در کتابها بود[4]. از همین اصطلاحها کمک میگیرم برای اینکه بحث جلو برود.این دستهبندیها کلی است، بعداً شما میتوانید مفصّل این ها را تقسیم کنید.
در عالم حس که همه بیداریم، حس میکنیم چیزی را میبینیم، وقتی چشم شما باز است دارید چیزی را میبینید.
شما الآن دو چیز دارید، یک محسوس متصل دارید، یک محسوس منفصل دارید. یک گلدانی که وسط این اتاق گذاشته ما دورش نشستیم، یک محسوس منفصل داریم که آن گلدان است. بیرون از ماست، به ما ربطی ندارد. اما ۷-۸ نفر که دور او نشستیم، محسوس متصل داریم؛ یعنی هر کدام از ما، سراغ آن محسوس منفصل میرویم، امّا دریافت ما از آن محسوس منفصل، یک جور نیست. شما آن طرفِ گلدان را میبینید، من، این طرفِ گلدان را میبینم، من از یک جهت دارم نگاه میکنم، شما از یک جهت دیگر. این مثال خیلی روشن است. پس ما در مرحله حس، محسوس منفصل داریم و محسوس متصل.
در این محسوس متصل و منفصل خیلی بحث است. شما این را یک کلام فرض نگیرید.
میآییم در خیال.
مثالی که مرحوم مظفر رضوان الله علیه زدند[5]. فرمودند این ساعت را شما نگاه میکنید بعد چشمتان را میبندید، همان ساعت را در ذهنتان میآورید. ساعتِ خارجیِ محسوسِ منفصل داریم، وقتی چشمتان باز است دارید ساعت را میبینید، این محسوس متصل است. وقتی چشمتان را بستید، بعدش صورت او را احضار کردید، به این میگوییم خیال متصل. الآن دیگر چشم شما باز نیست، ساعت را نمیبینید. چشمتان بسته است و دارید ساعتی را که دیدید احضارش میکنید؛ این میشود خیال متصل. یعنی صورتی از ساعت که الآن چشم شما باز نیست؛ امّا در خیال متصل شما ایجاد شده است.
اما خیال منفصل چیست؟ خیال منفصل، این است که محسوس نیست، عالمِ ماده نیست. اما در عین حال بند به نفْسِ شما هم نیست؛ خیال منفصل، هر چیزی است که شکل دارد، رنگ دارد، آثار ماده را دارد، اما هیولی و آن حرکت ناسوتی[6] را ندارد. یعنی یک مَلَکی را فرض بگیرید، متعلّق به عالم ملکوت.
خوابها هم انواعی دارد[7]. خیلی از خوابها، تمثّلِ نفْس است که خیال متصل است. اما خوابهایی انسانها دیدند که برای خودشان هم واضح میشود که من واقعاً در عالم دیگر بودم؛ همینطوری که اینجا داریم حرف میزنیم. خوابهایی که روحم در عالم دیگر میرود، دارد یک چیزی در عالم میبیند.
خوابهایی که فقط تمثّل است، خیال متصل است. اما خوابهایی که خیال منفصل است که یعنی روح در عالم مثال میرود. آنجا چطور؟آن جا ما یک متخیَّل منفصل داریم، یک تلقّی که من در خواب از آن مثالِ منفصل دارم؛ یعنی همانجا هم باز دو امر دارم: مثال منفصل، مثال متصل.
در عالم مثال، سروکار ما با فرد است، شما مثلث را میگویید شکل است؛ اما مثلثی که در قوه خودتان ایجاد میکنید، فردی از مثلث است. طبیعیِ مثلث نیست. قوّه خیال، سروکارش با طبایع نیست. شکل مثلث که در ذهن شما میآید، فردی از مثلث است.
بچهای که معلم در کلاس به او میگوید «مثلّث»، تا قوّه درّاکهی بچه یک سه ضلعی در ذهنش نکشد نمیتواند اصلاً حرف استاد را تصور کند. یعنی قوهی خیال، معین عقل اوست. اوّل باید قوه خیال بچه، یک مثلث بکشد بعد بگوید آقای معلم! حالا بگو تا من این را تطبیق بدهم. این بچه وقتی دبستانی است باید قوه خیال او مدام یک مثلث بکشد تا حرف استاد را بفهمد؛ همین بچه دانشگاه میرود، یک ساعت استاد ریاضی برایش حرف زده، بیرون میآید، میبیند استاد او ۳۰۰ بار مثلث گفت، اما وقتی به خودش برمیگردد میبیند یک بار قوه خیال او مثلث را نکشید. چرا؟ چون قبلاً قوه درک معانی او در درک معنای مثلث ضعیف بود. قوه خیال باید او را کمک می کرد؛ اما حالا قوی شده، نیازی ندارد قوه خیال او را کمک کند در احضار معنای مثلث. استاد میگوید مثلث، معنای او را هم میفهمد، هیچ مشکلی هم ندارد[8].
حوزه عقل
این برای مشاعر. اما بعدش عقل. عقل سروکارش با کلیات است، با طبایع است.
در فضای عقل، ما یک معقول منفصل داریم، یک معقول متصل. هنر، این است که ما اینها را در ذهن خودمان با مثالهای زیبا از همدیگر جدا کنیم که چشم همه ببیند.
الآن ببینید نوع مردم اصلاً توجه ندارند که ساعت در ذهنشان میآید. اما وقتی دقیق مثال میزنید، میگویید چشمت را به ساعت باز کن، بعد چشمت را ببند، صورتش را در ذهنت بیاور، با همین مثال زدن، چیزی که قبلاً در ذهن او بود، اما منحاز نبود منحاز شد. الآن هم ما میخواهیم همین کار بشود.
ما دو نوع بی نهایت درست و حسابی، داریم:
بی نهایتهای متعیّن افزایشی؛ بی نهایت های بسیار بزرگ[9].
بی نهایتهای متعیّن کاهشی؛ بی نهایت های بسیار کوچک[10] .
از زمان ارسطو، تمام بی نهایت ها، چه بی نهایت بزرگ و چه بی نهایت کوچک را با بی نهایت بالقوّه حل می کردند.
بی نهایت بزرگ را می گفتند: لایقف .
بی نهایت کوچک را می گفتند: بالقوّه . ما هم با این دوتا خیلی مانوس هستیم چون مبنای کتابهای ما هم معمولاً ارسطویی است. انسان خودش را قانع میکند به بی نهایتِ لا یقفی و کار تمام میشود[11].
اما از حدود 200 سال قبل تا حالا که ریاضیات عالی و آنالیز[12] کاملا پیشرفت کرده و مباحثش امروز برای بشر مثل خورشید شده،
واضح است که در بی نهایت کوچک، بی نهایتِ بالفعلِ نفس الامری است.می توانم بگویم بینهایتِ مجسّم، بینهایتِ در مشت. میگوید بیا، بینهایتِ بالفعل را در مشتت میگذارم و جلوی چشمت میآورم؛ بالاتر از این میخواهی؟!
[ما یک نسبت به معنای مطلق رابطه داریم،یک نسبت و رابطه داریم که فوق و ورای مقولات است؛
«مطلق رابطه». رابطه نفس الامری بین هر چیز و هر چیز می آید. بین کم و کیف می آید .بین جوهر و عرض می آید.این را هم ما اسمش را می گذاریم «نسبت و رابطه به معنای عام نفس الامری». خودش از لحاظ تحلیل مباحث بسیار ظریفی دارد و یکی از براهینی هم که در آن مقاله عرض کردم[13] برهان فرارابطه است. آنجا که عرض کردم «فرارابطه»، یعنی این رابطه؛ رابطه عام نفس الامری که ورای مقولات عشر است. اجناس عالیه بینشان می تواند رابطه می تواند برقرار باشد. رابطه نفس الامری که ما به الاشتراک ذاتی، دو تا جنس الاجناس ندارند.مثلا کم با کیف هردو جنس الاجناسند ما به الاشتراک در جنس ندارند.ما به الاشتراک ذاتی ندارند اما یک نحو اشتراکاتی نفس الامریِ وراء مقوله و ماهیت دارند. علی ای حال می بینیم یک نحو اشتراک دارند.هر دو در وصف امکان اشتراک دارند.ممکن الوجودند.کم ممکن الوجود است کیف هم ممکن الوجود است.در این وصف اشتراک دارند.بگویید امکان که جنس و ذاتی نیست، نباشد سلّمنا؛ ولی خلاصه یک رابطه اشتراکی بینشان هست.این رابطه به معنای عام را کنار بگذارید.
یک نسبت دیگر داریم که نسبت مقولی است. یعنی در مقولات عشر هفت تا عرض داریم که به آن ها می گوییم: «اعراض نسبیه و مقولات نسبیه» این جا هم نسبت به کار می بریم. این نسبت دیگر در کم و کیف و جوهر نیست. فقط در هفت تا عرض است. این هفت تا مقوله نسبی در بدایة و نهایة و جوهر النضید و… بحثش شده است.آن هم باز مقصود ما نیست. اصلا بیرون از کم است.هفت تا مقوله نسبی بیرون از کم است.آن را هم بگذاریدش کنار.
بیایید وارد شوید درخصوص مقوله کم. وقتی وارد مقوله کم می شوید حالا در دل مقوله کم یک نسبت داریم.یعنی در عالم ریاضیات یک نسبت داریم خاصّ خود کم. نسبتی که بین مقادیر مطرح است؛ نه نسبت بین دو تا جوهر یا نسبت بین زمان و مکان و جِده و این ها. نه درست در مقوله کم، این نسبت مطرح است. سرو کار ما الان با این نسبت است. همان نسبتی که گفتم او را عمل تقسیم آورده است.عمل، خیلی نقش دارد.عمل تقسیم، بازگشت ضرب است. این عمل تقسیم باعث شده که در فضای مقادیر فقط نسبت مطرح شود. پس شما هر وقت در ریاضیات می گویید: «نسبت این مقدار با آن مقدار» اصلاً ذهنتان نباید برود به نسبت مقولات نسبیه یا نسبتی که به معنای رابطه نفس الامری عمومی است، خصوصا در عالم مقدار.
خب این نسبتی که در عالم مقدار است یعنی چه؟یعنی بازگشت عمل ضرب.اگر یک مقداری در مقدار دیگر ضرب شود نسبت حاصل ضرب به یکی از این دو تا عامل های ضرب، می شود تقسیم. اسم این تقسیم را ما می گذاریم «نسبت». و لذا اگر می گویید نسبت شش به دو می گویید چند می شود؟ می شود سه.یعنی خارج قسمت، ضرب در مخرج مساوی با صورت.(خارج قسمت×مخرج=صورت) سه دو تا شش تا.صورت همیشه دارد تقسیم می شود مقسوم است. مخرج، مقسوم علیه است.کسر شش دو تا مساوی سه، آن سه خارج قسمت است که عمل ضرب را برعکسش کرده ایم؛ این خیلی روشن است.این عمل تقسیم آمد و پیاده شد در مقادیرِ کم منفصل که عدد است و مقادیر کم متصل قار که هندسه است.
من یک مقدمه عرض می کنم. ببینید شما مثلاً یک ستونی دارید در ساختمان.یک خودکاری هم دارید کنار دستتان گذاشته اید. اگر بگوییم که این ستون را مثلا به هفت قسمت مساوی تقسیم کنید بلند می شوید با فرض خودمان به هر وسیله ای به هفت قسمت مساوی این ستون را تقسیم می کنید.بعد می گوییم خودکار هم دستتان است این را هم به سه قسمت مساوی تقسیم کنید.خودکار تقسیم شد به سه قسمت مساوی آن هم آن ستون بلند به هفت قسمت مساوی تقسیم شد.حالا بگویید خب آن هفت این هم سه پس نسبت ستون به خودکاری که دست شماست هفت است به سه. درست حرف زدیم؟آن را تقسیم کردیم به هفت قسمتِ مساوی، این را هم تقسیم کردیم به سه قسمت مساوی. پس نسبت هفت است به سه.درست گفتیم؟ نه؛ چرا؟
چیزی را که تقسیم می کنند واحدهایش باید برابر باشند.باید عادّ مشترک داشته باشند.بله اگر بیایید خود این خودکار را شروع کنید روی ستون بغلطانید ببینید چند خودکار است؟ بعد می گویید من این خودکار را که روی ستون بردم دیدم تعداد دفعاتش مثلا شد 15تا، حالا خوب شد.می گویید نسبت ستون به خودکار نسبت 15 است به یک.اینجا نسبت، 15 است به یک .آنجا اشتباه کردید که گفتید نسبت، هفت است به سه.چون واحدهای در تقسیم ستون به هفت، واحدهای مختلفی است با واحدهای در تقسیم خودکار به سه.غلط است که این دو تا را با هم بسنجیم. وقتی می توانید بگویید نسبت، که یک عادّی هر دو را بشمارد. و لذا وقتی خودکار ستون را شمرد، حالا خوب است؛ می گویید نسبت ستون به خودکار، نسبت 15 است به یک.نسبت خودکار به ستون، نسبت یک است به15.
حالا آمد و خودکار را گرداندید و رفتید شد 15.5.یعنی یک خرده ستون بلندتر است از 15تا ولی شانزده هم نیست. اینجا باید چه کار کنیم؟الان راه چیست؟می خواهیم نسبت برقرار کنیم.نسبت این ستون با خودکار چند است؟15 که نشد چون بیشتر دارد.16 هم نشد چون باز ستون کم می آوریم.این جا مجبور هستیم واحد عاد را کوچکش کنیم.مثلااگر 15.5 است از این خودکار واحد را 30 میگیریم.نصف خودکار را می گیریم واحد.حالا می گوییم کل این ستون 30. یعنی نصف او کاره شد.حالا با نصف خودکار می رویم جلو، وقتی رسیدیم به 15 چند تا نیم داریم؟سی تا. آن باقی مانده اش هم نیم است می شود یک.می شود سی و یک.بعد می گوییم نسبت ستون به خودکار، سی و یک به دو. چون الان خودکار را دوتایش کرده ایم.
حالا اگر به جای این که خودکار نصفش باشد، ثلثش بود خب اینجا مجبوریم مخرج را وسیع تر بگیریم. عاد را کوچک می کنیم.حالا آمدیم باز کمتر شد این واسطه،خلاصه می رویم در دل اعداد تا برسیم به یک واحد خیلی کوچکی که می گوییم مثلاً این چند ملیون-از میلی متر هم برویم جلوتر-یک صدمِ میلی متر، عادّ واحد شد.پس ستون نسبتش به این خودکار برقرار است، فقط خودکار و عددش رفته بالا.همان طوری که آن جا یک شد دو، الآن هم می گوییم مثلاً نسبت ستون به این خودکار، نسبت 50 ملیون است به هزار؛چون عاد ما کوچک شد، ولی علی ای حال نسبت برقرار است.
خب این که الان ذهن شریفتان آماده شده من این مقدمه را به آن ضمیمه کنم.در عالم مقادیر که می خواهیم تقسیم کنیم اگر دو تا مقدار نامتجانس باشد، نسبت برقرار نمی شود مثل سایر موارد. شما بین شیرینی با سیاهی نمی توانید نسبت برقرار کنید.متجانس نیستند. نسبت شیرینی به سیاهی چیست؟نسبتی ندارند غیر از آن نسبت عامی که الان تقسیم بندی کردیم.نسبتی ندارند چون متجانس نیستند در این فضای ما .بله می توانید بالعرض نسبت برقرار کنید.بگویید مثلا سیاهی چند درجه دارد، شیرینی هم چند درجه دارد.این سیاهیش بیست درجه است آن ده درجه است.می گوییم نسبت بیست است به ده. خود این عدد را بالعرض، مشترک فرض گرفتید بین دو چیزی که با هم تشارک ندارند.علی ای حال طرفین نسبت، باید با هم متجانس باشند تا بتوانید بین این دو تا نسبت برقرار کنید.پس بین خط با سطح بین سطح با جسم تعلیمی با حجم نسبت برقرار نمی شود.همیشه بین دو تا خط نسبت برقرار می شود یا بین دو تا سطح نسبت برقرار می شود.نمی شود بگویند نسبت این خط به آن سطح چیست؟نسبتی ندارند.چون متجانس نیستند.این هم یک نکته خوب.
خب الان می آییم این جا ستونی که طول بود به عنوان یک خط، با خودکاری که باز به عنوان یک خط طول بود متجانسند یا متجانس نیستند؟متجانسند، لذا به راحتی بینشان نسبت برقرار کردیم با عاد مشترک.اما اگر نامتجانس باشند، این عادّی را که الان دنبالش هستیم ندارد.شما می گویید این خط چندتاست؟ می گویید مثلاً 5 سانتی متر. آن مربع چند تاست؟می گویید مثلا 7سانتی متر مربع.واحدِ این، مربع است و واحد آن، طول است.عادّ مشترک ندارند که بخواهد آن تقسیم بر این شود.
از عجایب کاری که اینجا کشف شد و بحران اول ریاضیات را صورت داد این بود. ارتکازاً همه ریاضیدان ها می گفتند خلاصه وقتی ما دو تا خط مستقیم داریم نسبت بین خط کوچک تر و بزرگ تر و کوچک تر و بزرگ تر برقرار می شود. به چه معنا؟یعنی خلاصه می رویم تا به یک عادّ کوچک بسیار ریز می رسیم که خطّ بزرگ تر را ملیون ها بار می شمرد و خطّ کوچک تر را هزارها بار. باورشان نمی شد که ما می توانیم دو تا پاره خط مستقیم داشته باشیم که این دو تا متجانسند -چون هردو خط مساویند- اما متباینند.
متشارک، متباین؛ متشارک یعنی عادّ برایشان پیدا می شود ولو خیلی ریز. اما این ها در پیشرفت ریاضی رسیدند به دو تا خط که اگر تا بی نهایت هم جلو بروید، به یک جزء بسیار ریزی که حتی در بی نهایت، عادِّ هر دو باشد و عدد صحیح، نمی رسید. این واویلا بود.این معنایش چه بود؟معنایش این بود که نمی توانستید بگویید نسبت او به او. چون الان وقتی شما واحد را خودکار می گرفتید و 15.5می شد، مجبور بودید چه بگویید؟ بگویید نسبت ستون به خودکار 15 به یک است ؟نه.«15و خرده ای» به یک است.تا یک عادّ مشترک پیدا نمی کردید، دقیقاً نمی توانستید بگویید نسبت. در ریاضیات که خرده ای نیست.ریاضیات باید جواب روشنی به شما بدهد که مطلوب معلوم شود. کشف مقادیر متجانس اما غیرمتشارک-یعنی عادّ مشترک ولو تا بی نهایت جلو بروید برای او پیدا نشود-این همه دم و دستگاه نسبت تناسب را به هم ریخت.
خب حالا یک مثالی می توانید برای ما بزنید؟بله قاعده فیثاغورث برایشان معلوم بود.مجموع مربّع دو تا ضلع برابر است با مساحت مربع وتر.
حالا یک مربع رسم کنید و قطرش را بکشید.مربع یک ضلع اگر فرض بگیریم یک واحد است.این یک واحد، مربعش هم می شود یک در یک. مساحتش می شود یک.
آن ضلع مجاور آن هم یک است؛ چون مساویند. مربع است دیگر.آن ضلع مجاور هم مربعش یک در یک،مساحتش می شود یک.پس دو تا مساحت دارید هر دو یک متر مربع.قاعده می گوید پس مربع قطر مربع وتر این مثلث قائم الزاویه برابر است با مجموع مساحت دو تا مربع.این دو تا مربع مجموعش چند می شود؟یک و یک می شود دو. پس مربع وتر ما مساحتش می شود دو.
متباین یعنی چه؟متباین یعنی اگر می خواهید بگویید نسبت قطر به ضلع، باید عادّ مشترک داشته باشند.تا بی نهایت اگر بروید به یک خط بسیار ریزی نمی توانید برسید که بگویید مثلا قطر n میلیارد بار است ضلع هم n میلیون بار است. کوچک تر است از او دیگر! این بود که خیلی کشف عظیمی بود و بحران درست کرد چه بحرانی! تناسب را به هم ریخت.دم و دستگاه تقسیم تمام شد دیگر.در تقسیم می گفتند نسبت مربّع قطر وتر به ضلع چند است؟همین الان ما که می گوییم 2 جذرش را بگیر.جذر 2 می شود ١/۴١۴ بروید عدد اعشاری تا بی نهایت. یعنی نمی رسید به صفر، دائماً باید بگویید تقریباً.تقریبا هم که تقسیم نشد.نسبت نشد.
لذا ریاضیدان ها الان این کار را می کنند؛ عدد را با یک نماد ترکیبی می گویند.می گویند: «جذرِ دو» ببینید خود «دو» را می آورند، آنی که اگر ضرب در خودش بکنیم و به توان دو برسانیم، می شود دو. چون مربعش را داریم.مربعش موجود است و جلوی چشم ماست.ضلعش هم جلوی چشم ما موجود است.همه این ها را داریم.کاری هم نمی توانیم بکنیم در هندسه.چه عددی است؟عدد ندارد. آقای فیثاغورث! فیثاغورثیان! چه طور گفتید نظام عالم بر عدد است؟عدد مقدس است که همه عالم را ساخته است؟! قطر مربع، جلوی چشم ما هیچ عددی نمی تواند نشان بدهد ولوتا بی نهایت برویم.عددی نداریم.فقط باید بگوییم جذر دو.یعنی همانی که مبهم و مجهول است. اصلاً نیست. می گوییم نه! این که خطش را دارید می بینید.مربعی را هم که تشکیل داده است، دارید می بینید. اما قطر مربع -این وتر مثلث قائم الزاویه با دو ضلع واحد را- نمی توانید بگویید چند است؟ هیچ عددگویا ندارد.حتی نسبت بین دو تا عدد نمی تواند باشد.
گنگ بودن جذر دو، رادیکال دو، این که ریشه دو محال است،برهان های متعددی دارد. ؛ در اینترنت ببینید. می گویند خلاصه باید یک جایی باید برسد که به صورت نشانش بدهیم.می گویند لازمه این که بخواهد جذر او باشد این است که a حتما زوج باشد، b هم حتما زوج باشد و این خلف فرض است.از طریق برهان خلف می گویند اصلاً محال است رادیکال 2 را به صورت نسبت دو عدد a,b نشانش بدهید.خلاصه یا زوج است یا فرد. از این که بیرون نیست. با برهانی که می گویند، لازمه اش این است که هردویش زوج باشد و وقتی هر دویش زوج بود کسر ساده ای که ساده ترین کسر باشد، نیست. چند تا برهان برایش می آورند[14].]
بینهایت، انواعی دارد. یک مثال روشنش، عدد پی( )[15] است. عدد پی، عددی هندسی است، یعنی شما اوّل سروکارتان با دایره میشود. دایره چیست؟ یک خطِّ بستهی منحنی. خط برای کجاست؟ برای هندسه است؛ کمّ متصل قارّ. دایره یک مرکز دارد. مرکز، نقطه است. نقطه، عنصر هندسی است. قطر چیست؟ خطّ مستقیمی که از مرکز رد میشود و دایره را دو قسمتش میکند. این خطّ مستقیم، طول است؛ کم متصل قارّ است.
میخواهیم ببینیم نسبت محیط دایره به قطر چقدر است؟ یعنی اگر محیط را باز کنیم، از گِردی در بیاوریم و یک خطِّ مستقیمش بکنیم، چند تا قطر بگذاریم سر میرسد؟ می گوییم سه تا قطر را که روی محیط بغلطانید، دایره می گردد[16]، دفعه بعدش دیگر نه؛ کمی از آن فقط میماند. این را میگوییم نسبت محیط به قطر، یعنی محیط، چند برابر قطر است؛ نسبت یعنی صورت، تقسیم بر مخرج. یعنی محیطِ گردِ دایره، تقسیم بر قطر، می شود عدد پی.فعلاً میگوییم ١۴/٣.
هر دایره دلخواه را –که دایره هندسی باشد- روی هر محوری رسم کنید، به محض اینکه روی محور اعداد، این دایره را باز کنید، اگر قطر این دایره،١ باشد(«یکِ» رویِ محور) یک سر محیط دایره را روی عدد صفر میگذارید، آن سرِ محیط میشود عدد پی[17]. یک نقطهی معیّن روی محور؛سه و چهارده صدم و …بروید تا بینهایت.[18]
[آیا خط مستقیم با خط منحنی دو جنس هستند یا یک جنس هستند؟ خلاصه طول هستند. در اینجا روی یک نگاهی که همه دارند و پذیرفته شده است، خط منحنی با خط مستقیم از حیث کمّیت طول متجانس هستند، ولذا در دایره، محیط آن منحنی است اما قطرش خط مستقیم است؛ میگویید نسبت محیط دایره به قطر سه و چهارده صدم است. یعنی میتوانید قطر را سه بار روی محیط دایره بغلطانید که مقادری هم زیاد میآید؛ سه و چهارده صدم. محیط سه برابر و خوردهای از قطر خودش است. قطر ضرب در سه و چهارده صدم نزدیک به محیط دایره میشود. خُب این نسبتی شد بین دو کمیت متجانس؛ نسبت محیط بر قطر.
این چه نسبتی است؟ متباین است یا متجانس است. این خیلی طول کشید. خُب قطر مربع دو هزار و پانصد سال پیش معلوم بود که متباین هستند. اما اینکه آیا قطر با محیط متباین هستند یا نه، تا حدود دویست سال پیش آمده است. یعنی این قدر در تاریخ طول کشیده تا بشر برهان بیاورد که نسبت محیط با قطر نسبتی است که تا بینهایت میرود و اصم است؛ به یک عاد مشترک واحد نمیرسند[19].]
عدد پی، عددی است که روی نقطه معیّنی روی محور است، اما شما نمیتوانید نشانش بدهید. چه کار میکنید؟ از پس و پیش، به آن نزدیک میشوید. یعنی از ۳.۱۴ که مثلاً با ۹۶ ضلعی ارشمیدس بوده[20]، از نقطه ۳.۱۴ شروع میکنید، بعد از ۳.۱۴ روی محور، ۳.۱۵ است. میگویید نقطه پی که محیط دایره است، بین ۳.۱۴ و ۳.۱۵ هست. نه بیرون از ۳.۱۵ است، نه عقبتر از ۳.۱۴ است؛ بین این دو تاست. از طرفین(۳.۱۵ و ۳.۱۴ )به آن نزدیکتر میشوید وتا بینهایت میروید. حدّش[21] هست. به تعبیر مسامحی میگوییم در بینهایت به پی میل میکند.
امروز دیگر اینها از واضحات است، یعنی اهل خبره دو نفرشان هم در این اختلاف ندارند، امروز برای بشر، این که عدد پی عددی است گنگ[22]، متعالی[23]و رسمناپذیر[24] [25] ، اینها همه مبرهن شده است[26].
خوب دقت کنید. الآن عددهای بعد ۱۴ صدُم را؛ممیّزهای بعد ممیّز را، تا چندین تریلیون حساب کردند[27]. خلاصه آخرین عددی که فعلاً بشر میداند، میدانیم یک عددی معیّن بعدش هست؛ ما نمیدانیم، ولی معیّن است. ما باید برویم کشفش کنیم؛ نه فرضش کنیم؛ نه خلقش کنیم .نکته اصلی این است، این نقاطی که شما بعد از ممیّز میگذارید، نقطهای معیّن روی محور است؛ نقطهی نامعین نیست. یعنی ۳.۱۴ که معین است، عدد بعدی ممیز که ۳.۱۴۱، روی محور معلوم است، ولو نزدیکتر به پی شده ولی خود پی نیست. عدد بعدی هم همینطور، تا بینهایت میروید ولی به سر دایره نمیرسید، چون عدد گنگ است. ولی نقاطی که طی میکنید تا به آن نزدیک بشوید نقاط متعین است.
این است که میگویم زمینهاش فراهم است که برای بشر نشان بدهیم. الآن شما یک دایره را باز کردید، کف دست بچه میگذارید. میگویید این سر «پی» که معلوم است، صفر هم معلوم است. وقتی میخواهی حساب کنی بروی برسی به سر دایره که پی است، در رسیدن به نقطهی پی، بینهایت نقطهی متعیّن است که هر چه حساب پی را جلوتر ببرید کشفش میکنید.دو طرف، بینهایت. یعنی از دو طرف دارید به آن نقطه پی نزدیک میشوید تا بینهایت هم در بینهایت نزدیک میشوید، نقاطش هم متعین است، شما کشفش میکنید؛ ولی در عین حال هیچکدام از آنها «پی» نیست!این،یک مثالِ هندسیِ ساده است، هر بچهای هم در دبستان خوانده است. میخواهیم چیزهایی را که همه بلد هستند فقط به او نشان بدهیم.
الان این مثال،مثل سنگ خاراست، فقط باید کار بشود و این مثالها باز بشود،تصویری توضیح داده بشود، که همه بفهمند. وقتی اذهان مطلب را گرفتند، همینطور دست به دست میشود؛ به سرعت پخش میشود.
آیا وقتی شما میگویید یک دایره محیطش با قطرش، نسبتی دارد، واقعاً این شکل(شکل دایره که یک خط است و این نقطه مرکزش است) چه کسی است که آن را به وضوح درک نکند؟ همه میفهمیم شکل چیست؛ درک روشنی از آن داریم.
سؤال این است:
– وقتی میگوییم نسبتِ دایره به قطر، منظور ما از این دایره، کدام دایره است؟ دایرهای است که فقط در ذهن شماست یا در ذهن من است؟ دایرهای که در دفترِ شما کشیدند یا دایرهای که در دفترِ من کشیدند؟ کدام دایره؟ همهی این ها روی هم؟
یعنی اگر هر چه دایرهی کشیده هست یا ذهنهای همه بشر یک دفعه محو بشوند، نسبت محیط دایره به قطرش تمام میشود؟ اینکه محیط دایره سه برابر قطرش است، این نسبت دیگر نیست؟ محو میشود؟ یا نه؛ ذهن و عقل ما این نسبت را درک میکند.
اگر هیچ انسانی نباشد، ولی یک شیئ تیزی بیاید و یک سنگی را که به صورت گردی هست ببرد، مقطع این سنگِ گردِ توپمانند، دایره نیست؟ دایرهی مادّی. اتصاف او به این گِرد بودن به ذهن ما ربطی دارد؟
وقتی شما یک توپ را نصف میکنید، نصف شدن توپ، بند به ذهن شما نیست. و حدوث مقطع یک توپ به عنوان سطحِ دایره، باز به ذهن شما مربوط نیست. یعنی شما میتوانید دایرهای در بطن ماده پیدا کنید.الان من چیزی را درک میکنم گرد است یا من به آن میگویم گرد است؟ اگر گفتن است ،بگویید مربع است؛ یک اقوامی بگویند این چهارگوش است، یک اقوامی بگویند گرد است.
شما میگویید: محیط، قطر، دایره، طول، فاصله، بُعد. وقتی طول میگویید، همه میفهمند: طول یک متری، یک سانتیمتری، یا بُعد: بُعد ۲ سانتی مثلاً.
وقتی میگویید طول، آیا مفهوم طول،هم طول دارد یا ندارد؟ چند متر است؟ طول، دیگر معنایش طول ندارد، اما مصداقش چرا، طول دارد.
فاصله؛ هر فاصلهای بینش دو نقطه است. هر فاصلهای اوّل دارد، آخر دارد، دو طرف دارد. آیا مفهوم فاصله هم دو طرف دارد یا ندارد؟ مفهومِ فاصله، دو تا لبه ندارد؛ مصداقش است که دو تا لبه دارد. مفهوم فاصله، در آن فاصله نیست. این ها مفاهیماند.
وقتی شما میگویید که فاصلهی بین مرکز دایره با محیط دایره، شعاع دایره است. الآن آیا این فاصلهای که شما به کار بردید، مفهومِ فاصله است یا مصداق آن است؟ این فاصله، مفهوم نیست؛ چون اوّل و آخر آن، دو تا نقطه است-از مرکز تا محیط دایره-واقعاً بین این دو، فاصلهی خارجیِ مصداقی است. اما اگر مصداق است پس چرا تعیّن ندارد؟ شما مفهوم کلی فاصله را طوری در نظر گرفتید که با افراد مختلف، صدق کند.
قطر، محیط، دو تا مفهوماند. نسبت بین این دو تا مفهوم از نسب اربعه چیست؟ تباین است؛ هیچ قطری محیط نیست و هیچ محیطی هم قطر نیست. این از حیث مفهوم، روشن است. دوباره شما میگویید نه. من که میگویم نسبت بین محیط با قطر، مقصودم بین دو تا مفهوم از حیث مصادیقشان نیست که میگویید متبایناند؛ من در یک دایره، نسبت سنجی می کنم. همین جا آیا باید دایرهی مشخصی باشد تا نسبت برقرار بشود؟ یا نه؛ در کلّیِ دایره بین محیط با قطر، نسبت برقرار میشود. کلّی به کلّی.
سؤال ما دقیق این است:
الآن که نسبت بین محیط با قطر کلی است، این قطر، این محیط و این نسبت این دو، به همین نحوی که الآن برقرار است، دارای شکل هستند یا نیستند؟ آن هایی که طرف نسبتاند، آن ها شکل دارند یا ندارند؟ اگر شکل دارند، مقدار باید داشته باشند. مقدارشان چه اندازه است؟ نامتعین است؟چطور شما یک شکلی دارید که اندازهاش نامتعین است. مگر ما شکل کلی هم داریم؟
اصلاً شکل یک مفهوم عقلانی دارد. شکل، شکل ندارد. شکل، یک مفهوم کلی است.
اما مصداقش، یک دایره میشود. دایره، یک شکل است به حمل شایع. تفاوت این دو تا چیست؟ تفاوتش این است که شکل دایره به عنوان یک شکل، از عالم مثال منفصل است و لذا بین الاذهان است؛ همهی اذهان با هم در یک عالمی میروند که در منظر همه بشر است و آن را میبینند. آن عالم کجاست؟ مثال منفصل؛ مجرّد است به تجرد برزخی، آثار ماده را دارد ولی خود ماده را ندارد.
دایره ۲ متری، به ذهن شما بند است. دایره ۳ متری هم به ذهن دیگری بند است. اما شکل دایره -نه کلّیِ شکل که عقلانی است- شعاعش چقدر است؟ شکل دایره، قطرش چند متر است؟ اتفاقاً آن هایی که هندسه درس میدهند میگویند دایرهای با قطر واحد، یا دایرهای با شعاع واحد. پس در علم هندسه به راحتی شکل دایره را درک میکنند. شکل هست، ولی تعیّنِ مقدارِ خاصّی از شعاع و قطر نداریم.
به محض اینکه یک دایره را شعاع مِتریک به آن بدهید، بگویید ۲ متر، ۳ متر، متشخّص شد؛ شد یک فرد دایرهای که در قوهی خیالِ متصل موجود است. یعنی ذهن شما یک شعاع خاصی را به آن داد، حالا شد خیال متّصل.
پس شکلِ دایره، شکلِ مربع، یک طبیعی است که خودش را در ضمن کمّ متصل قارّ در عالمِ مثالِ منفصل به ذهن ما نشان میدهد. اما ما چون الآن داریم او را به راحتی میبینیم، مثل بچهای هستیم که هنوز تشخیص نمیدهیم که آن شکل منفصل برای عالم مثال منفصل، با آن شکل برای مثال متصل که تصور میکنم تفاوت دارد.
–ما عالم مثالی که میشناختیم و در درس خوانده بودیم، فرد بود. عالم مثال هم فرد دارد و هم طبیعی[28]؟
اینجاست که قدر این روایت را میدانید؛ خود عالم مثال، ۱۸۰۰۰ عالم است[29]. ما هنوز می خواهیم با یک زحمتی دوتایش را تفکیک کنیم. ۱۸۰۰۰ عالم است. عوالم با هم فرق دارند.
من نمیخواهم چیزی را ثابت کنم. میخواهیم آن چیزی که همه داریم ببینمش. ما وقتی در هندسه میگوییم نسبت محیط به قطر، محیط قطعاً کم است، خط است، طول است. اما چند متر؟ طولی است که متر فیزیکی ندارد. نمیخواهیم بگوییم چند متر است. قطعاً طول است، قطعاً تجرد تام نیست. چرا؟ چون طول شکل دارد و در قوه خیال ظاهر میشود. شکل دایره در قوه خیال حاضر میشود. اما این شکل دایرهای که احضارش میکنید، شما با عقلتان در مثال منفصل شکل دایره را میبینید. چند متر است؟ مثال منفصل، متر نمیخواهد. طول میخواهد، خط منحنی میخواهد، اما اندازه نمیخواهد. وقتی به عالم فیزیکی میآید اندازه میخواهد.
ما طول مبهم داریم یا نداریم؟ اینکه همین ابهام سبب بشود برای نفی چنین صورتی در عالم مثال منفصل و ما بگوییم قطعاً این طول در عالمِ مثالِ منفصل نیست، این ملازمه و سببیّت برقرار نیست.
به خاطر اینکه عوالمی در مثال منفصل هست-اینطور که گفته اند و مدعی شده اند- که آن تفرّدِ فیزیکیِ خارجی را خیلی نیاز ندارد. یادم میآید مرحوم میرزا جواد آقا ملکی تبریزی فرموده بودند که به یک میوه وقتی در عالم مثال نگاه میکنید، میوه در عین حال که سیب است، در همان حال پرتقال است. این برای ذهن ما الآن سنگین است.[30]روایت هم دارد. ذیل بحث میوه ممنوعهای که حضرت آدم(علیه السلام) خورده است، بعضی میگویند خرما است، بعضی میگویند گندم است، انگور است حضرت فرمودند که همه این ها هست[31].
خلاصه نمیشود احکامِ اینجا را بر آن ها جاری کرد. یک میوه را وقتی نگاهش میکند، هم سیب است هم پرتقال است. ما الآن میگوییم معقول نیست؛ تناقض میشود؛ اجتماع ضدین میشود.این را فقط اشاره مطرح کردم که اینطور ادّعا و نظر هست که عالم منفصلی از مثال داریم که خیلی احکامی که اینجا داریم، لازم نیست آنجا باشد. و لذا دایرهای که طولش مبهم است، در آنجا یک امر محالی نیست، ولی در عین حال شکل است، طول دارد؛ خواص ماده را دارد، ولی مادّیت مادّه را ندارد.
مثالهای ما این را واضح کرده که شکل دایره، حتماً یک واقعیت منفصلی دارد، ولی این واقعیت منفصل تجرّد برزخی دارد؟ یعنی آثار ماده از شکل و طول و عرض و رنگ دارد که مثال منفصل بشود؟ یا نه، آن واقعیتی که دارد از سنخ معناست؛ از سنخ معنایی که به قوه خیال ما این طول و عرض و خواص مادّه را دستور میدهد.
تأمل کردم، دیدم احتمال قویای است- نمیشود از کنارش رد شد-که این شکل به عنوان یک موجودِ نفسی در ذهن ما اصلاً معنا نداشته باشد. یعنی ذهنِ من و شما همه ،یک معانی ای مرکب که همهاش از سنخ طبایع است، به عنوان فرمولی از معنا دارد که تا میگویید: «علامت جمع[32]»، فوری در قوّهی خیالتان، یک علامت جمع ترسیم میکند. راسِمَش، یک معنایی است که عقلتان درک کرده است. اگر آن معنای درکی را نداشتید، قوّه خیال شما، قوّهی این که آن را ترسیم کند نداشت.
عکسهایی هست که همه در موبایلهایتان دارید؛ از سنخ اس وی جی(SVG) [33]. اگر کد این ها را ببینید، جز چند تا فرمول هیچ چیز دیگری نیست، صفحهی مانیتور موبایلتان یا کامپیوترتان را تقسیمبندی کردید، با فرمول به آن میگویید این طور در مانیتور، عکس بکش، از اینجا به آنجا بکش. یک تصویر در میآید. ذهنِ ما در خزانهی معانی خودش، یک فرمولِ معنایی دارد، حتّی بچهای که در ذهنش، مثلّث میکشد، آن معناست که به او اجازه میدهد که بتواند در ذهنش یک مثلث رسم کند.
مثالهایش را هم شما شبیه این دستگاه های امروزی ببینید، آن که در دلِ حافظهی کامپیوتر و موبایل است، نقش نیست، در دل آن، هرگز علامت جمع نیست، اما یک فرمولی، یک نظمی در دل حافظهی او هست که نرم افزار وقتی به آن فرمول نگاه میکند، به صفحه نمایش دستور میدهد این علامت جمع را وضع کن. از نقطهی فلان بکش به نقطه دیگر؛نگاشت ریاضی.
لفظ نگاشت دو جا به کار میرود:
این مفهوم دوم را نمیشود اینجا بگویند.مقصود ما در اینجا، نگاشت ریاضی[35] است. مثل این که دستگاه شما آن چیزی که دارید در مانیتورش میبینید، فرق دارد با این دستگاهی که دیگری دارد در مانیتورش میبینند. گرچه آن مطلبی که در حافظه دستگاه شماست، یکی است، ولی مانیتورها دو تاست، یعنی دستوری که دستگاه شما میدهد که نگاشت کن، در مانیتور با آن فرق میکند.
با این حساب، برهانِ ما فعلاً اثبات نکرده که یک نقشی منفصل داریم که آن را از مثالِ منفصل، احضار کنند و به چنگ بیاورند.
ما آن را که به وضوح داریم، یک معنای منفصل[36] است از آن نقش. این معنا را من و شما، همه داریم. به محض اینکه به آن معنا توجه میکنیم، آن معنا در صحنهی ذهن من و شما که به منزله مانیتور است، فوری میگوید یک بستر فراهم کن، رزلوشن درست کن، پیکسلهایش را بگذار، در آن پیکسلها این ها را حذف کن. یعنی خود معنا این دستور را میدهد.
سؤالات ما فعلاً یک واقعیت این چنینی را بهطور واضح، منفصل میکند. برایش اثبات میکند که شکی در آن نیست.منفصل یعنی اگر ما هم نبودیم، بود. انسان نبود، ذهن او هم نبود، این چنین بود. تمام کسانی که با مفاهیم هندسی و ریاضی آشنایی مختصر داشته باشند، حرف های ما را میبینند که در خودشان اینها را دارند ؛ نه این که برایشان اثبات بشود، اما مثال منفصل را نه؛ هنوز تا این اندازه فاصله داریم که بتوانیم نشان بدهیم که ببین! ما یک نقش منفصل داریم که او را فراچنگ آوردیم، ولی ما به مقصودمان رسیدیم. چون برایمان کافی است که بگوییم پشتوانهی این نقش، یک معناست.
[1] برشی از مقاله «مثال دقیق، سؤال روان؛ ابزاری برای ارائه مجردات به همگان». در تنظیم مطالب بالا هم چنین از جلسه سوم تاریخ و مباحث ریاضیات و جلسه هشتم فقه هوش مصنوعی نیز بهره گرفته شده است که با قرار گرفتن در داخل کروشه متمایز شده اند.
[2] والمَشَاعِرُ:الحواسُّ.قال بَلْعاءُ بن قيس:
و الرأسُ مرتفعٌ فيه مَشَاعِرُهُ —- يَهْدِى السبيلَ له سَمْعٌ و عينان (الصحاح،ج2،ص:699)
و هو ذَكيّ المشاعر و هي الحواسّ.( أساس البلاغة ؛ ص331)
و المَشاعِرُ: الحواسُّ (لسان العرب ؛ ج4 ؛ ص413)
و منه الْحَدِيثُ” بِتَشْعِيرِهِ الْمَشَاعِرَ عُرِفَ أَنَّهُ لَا مَشْعَرَ لَهُ” . و مِثْلُهُ” لَا تَشْمُلُهُ الْمَشَاعِرُ” . و شَوَاعِرُ الإنسان و مَشَاعِرُهُ: حواسه و منه (مجمع البحرين ؛ ج3 ؛ ص349)
در روایات نیز چنین آمده است: بتشعيره المشاعر عرف أن لا مشعر له (الكافي (ط – الإسلامية) ؛ ج1 ؛ ص139)
و همین طور:لا تشمله المشاعر(همان، ص١٣٩-١۴٠)
در نهج البلاغه نیز آمده است: لا تستلمه المشاعر(نهج البلاغه،٢١٢)و در برخی نسخ لا تلمسه آمده است(شرح ابن ابی الحدید،ج ٩،ص ١۴٨)
[3] الشيء قد يكون محسوسا عند ما يشاهد ثم يكون متخيلا عند غيبته بتمثل صورته في الباطن كزيد الذي أبصرته مثلا إذا غاب عنك فتخيلته و قد يكون معقولا عند ما يتصور من زيد مثلا معنى الإنسان الموجود أيضا لغيره(الاشارات و التنبیهات،ص ٢٣٨)
[4] أنه تبين بما تقدم أن الوجود ينقسم من حيث التجرد عن المادة و عدمه إلى ثلاثة عوالم كلية :أحدها عالم المادة و القوة .
و ثانيها عالم التجرد عن المادة دون آثارها من الشكل و المقدار و الوضع و غيرها ففيه الصور الجسمانية و أعراضها و هيئاتها الكمالية من غير مادة تحمل القوة و يسمى عالم المثال و عالم البرزخ لتوسطه بين عالمي المادة و التجرد العقلي و قد قسموا عالم المثال إلى المثال الأعظم القائم بنفسه و المثال الأصغر القائم بالنفس الذي تتصرف فيه النفس كيف تشاء بحسب الدواعي المختلفة فتنشئ أحيانا صورا حقة صالحة و أحيانا صورا جزافية تعبث بها .
و ثالثها عالم التجرد عن المادة و آثارها و يسمى عالم العقل.(نهایه الحکمه،ص: ٢۴۵)
شهرزوری در تفکیک عالم مثال متصل از منفصل چنین می گوید: و بعض المشايخ ممن يقول بثبوت العالم المثالي يقول: إنّ الخيال حصّة من عالم المثال يجري منه مجرى الجدول من النهر العظيم و يسميه ب «الخيال المتصل» و يسمى عالم المثال ب «الخيال المنفصل».( رسالة في العلوم الإلهية و الأسرار الربانية (الشجرة الإلهیة)، جلد: ۳، صفحه: ۴۶۶-۴۶۵)
محقق دشتکی می گوید: و الخيال إمّا متّصل أو منفصل؛ و لكلّ تفصيل.و من الصوفية من زعم أنّ الخيال المنفصل هو عالم المثال؛ و الخيال المتّصل القوّة الخيالية الإنسية؛ و ما يتخيّل بها و لا يشاهد هو المثال المقيّد؛ و ما يشاهد من ذلك العالم مثال مطلق.و توضيحه: أنّ للقوّة الخيالية الإنسية أن يتخيّل مثلا جبلا من ياقوت؛ فالخيال أو التخيّل و المتخيّل كلّ باعتبار خيال متّصل؛ و ما يخيّله مثال مقيّد؛ و إذا رأى راء في منامه جبلا من ياقوت و شاهده كان المشاهد مثالا مطلقا؛ و هو أو ما شاهد به أو الشهود كلّ باعتبار خيالا منفصلا.( إشراق هیاکل النور لکشف ظلمات شواکل الغرور، صفحه: ۲۵۹)
میرداماد نیز چنین می فرماید: قومى از رواقيّۀ فيثاغورسيّين و افلاطونيّين ، و رهطى از اشراقيۀ اسلاميّين ، عالمى متوسّط ميانۀ عالم غيب – كه عالم معقول – و عالم شهادت – كه عالم محسوس است – اثبات كردهاند؛ وآن را هورقليا و عالم مثال و عالم شهادت مضاف و عالم اشباح و عالم برزخ و اقليم ثامن و ارض حقيقت و خيال منفصل ناميدهاند ؛ و خيال انسانى را خيال متّصل.( جذوات و مواقیت، صفحه: ۶۲)
در کلمات مکنونه نیز چنین آمده است: و ما من موجود محسوس او معقول الاوله مثال مقيد فى هذا العالم البرزخى ، فهو فى العالم الكبير بمنزلة الخيال فى العالم الانسانى الصغير، فمنه ما يتوقف ادراكه على القوى الدماغية و يسمى بالخيال المتصل ، و منه مالا يتوقف على ذلك، و يسمى بالخيال المتصل (کلمات مکنونة من علوم أهل الحکمة و المعرفة، صفحه: ۷۰)
همین طور ببینید: المظاهر الإلهیة في أسرار العلوم الکمالیة، صفحه: ۸۹، الحکمة المتعالیة في الأسفار العقلیة الأربعة، جلد: ۱، صفحه: ۳۰۲و شرح و تعلیقه صدر المتالهین بر الهیات شفا (ملاصدرا)، جلد: ۱، صفحه: ۵۹۰و محبوب القلوب، جلد: ۲، صفحه: ۲۷۲و و أنوار العرفان، صفحه: ۲۳۱و أسرار الحکم في المفتتح و المختتم، صفحه: ۴۰۹-۴١٠
برای مطالعه تفصیلی این موارد به پیوست شماره ٢ مقاله «مثال دقیق، سؤال روان؛ ابزاری برای ارائه مجردات به همگان» مراجعه فرمایید.
[5] و قد تسأل على أي نحو تحصل للانسان هذه الادراكات؟ و نحن قد قربنا لك فيما مضى نحو حصول هذه الادراكات بعض الشيء، و لزيادة التوضيح نكلفك ان تنظر الى شيء أمامك ثم تطبق عينيك موجها نفسك نحوه، فستجد في نفسك كأنك لا تزال مفتوح العينين تنظر اليه، و كذلك اذا سمعت دقات الساعة – مثلا – ثم سددت اذنيك موجها نفسك نحوها، فستحس من نفسك كأنك لا تزال تسمعها… و هكذا في كل حواسك.(المنطق،ص١۴)
[6] و تطلق على عالم الشهادة أي الدنيا(کشاف اصطلاحات الفنون والعلوم،ج٢،ص١۶٨٠)
فَعَلوت، صیغه مفید مبالغه است.ملکوت، مبالغه در ملکیت و سلطنت. تابوت، مبالغه در رجوع که دیگر بازگشت به دنیا ندارد.طالوت قدش خیلی بلند بوده است.جالوت خیلی بد بوده جولان داشته است .ناسوت مبالغه در ناس است.طاغوت، مبالغه در طغیان است.(از افادات استاد)
[7] الكافي، عن علي بن إبراهيم عن أبيه عن ابن أبي عمير عن سعد بن أبي خلف عن أبي عبد الله ع قال: الرؤيا على ثلاثة وجوه: بشارة من الله للمؤمن و تحذير من الشيطان و أضغاث أحلام. (بحار الأنوار (ط – بيروت) ؛ ج58 ؛ ص180)
كتاب التبصرة لعلي بن بابويه، عن سهل بن أحمد عن محمد بن محمد بن الأشعث عن موسى بن إسماعيل بن موسى بن جعفر عن أبيه عن آبائه ع قال قال رسول الله ص الرؤيا ثلاثة بشرى من الله و تحزين من الشيطان و الذي يحدث به الإنسان نفسه فيراه في منامه و قال ص الرؤيا من الله و الحلم من الشيطان.( همان، ص: 191)
مرحوم مجلسی در جلد ۵٨(طبع بیروت) بحار الانوار،بابی را با عنوان حقيقة الرؤيا و تعبيرها و فضل الرؤيا الصادقة و علتها و علة الكاذبة به این بحث اختصاص داده است.(شروع باب از صفحه ١۵١است) ایشان پس از ذکر احادیث مختلف،در بخش تفصیل و تبیین به بیان اقوال حکما و دیگر عالمان در تحلیل خواب و انواع آن می پردازد (ص ١٩۵) هم چنین در کتاب منهج الرشاد لمعرفه العباد نیز بابی با این عنوان وجود دارد: من جملة الشواهد على وجود العالم المثاليّ ما يشاهد في النوم(منهج الرشاد،ج ٣،ص ١١۶)
[8] در ادامه و در تحلیل عالم مثال منفصل مطالبی خواهد آمد که در آن رابطه عالم مثال با طبیعت تبیین شده است و تکمله این مباحث خواهد بود.
[9] به گزارش بیگ بنگ، ما اخیرا به دنبال بزرگترین عدد معنیدار در جهان گشتیم، اما همۀ اینها باید در مقایسه با بی نهایت بسیار خرد باشند. ریاضیدانان بی نهایت را با سختگیری بالایی تعریف می کنند. اما ما تعریف وسیعتر و رایجتری را مد نظر قرار خواهیم داد: بی نهایت هر عددی را شامل می شود که محدود یا متناهی نیست. خب حالا بگذارید ذهنمان را محدود نکنیم و به جزئیات بی نهایت بپردازیم.
آغاز بی نهایت
برای صحبت دربارۀ بی نهایت، باید در ابتدا راهی برای تعریف آن از منظر ریاضی پیدا کنیم که البته کار سادهای نیست. اگرچه مفهوم بی نهایت با یونانیان باستان شناخته می شود و در محاسبات آیزاک نیوتن و گوتفرید لایبنیتس لحاظ شده است، اما بی نهایت تا اواخر دهه ۱۸۰۰ میلادی به صورت جامع تعریف نشده بود. قبل از آن، بی نهایت صرفا یک مفهوم ِ گسترده و بی شکل بود؛ بیشتر مانند یک اثر هنری با عملیات ریاضی خاص، نَه چیزی که ارزش فهمیدن داشته باشد. در حقیقت، ریاضیدانان زیادی در قرن نوزدهم از بی نهایت بعنوان مفهومی ناخوشایند و مبهم یاد می کردند و باور داشتند که هیچ جایگاهی در مباحث ریاضی جدی ندارد. در بهترین حالت، بی نهایت موضوعی بود که میتوانست در میان فلاسفه به بحث گذاشته شود. در همین مضمون بود که «جورج کانتور» نخستین شواهد از وجود بی نهایت را در سال ۱۸۷۴ منتشر کرد. او که در روسیه به دنیا آمده و در آلمان بزرگ شده بود، شواهدی شگفتانگیز و بحث برانگیز ارائه داد که نه تنها ماهیت بی نهایت را تعریف کرد، بلکه حتی مشخص نمود که بی نهایتهای متعددی وجود دارد و برخی بی نهایتها بزرگتر از دیگری بودند. آنچه این دستاورد را بسیار قابل توجه کرد این بود که او کل شواهد را از یک شاخه باستانی و به ظاهر بیمصرف از ریاضی بدست آورده بود که به نظریه «مجموعهها» مشهور شد.
نظریه مجموعهها
نظریه مجموعه (Set Theory) به طرز خندهآوری ساده به نظر می آید، اما بعنوان یکی از قویترین ابزارها در ریاضی مدرن شناخته می شود. ایدۀ اساسی آن را می توان در کارهای ارسطو جستجو کرد که بیان می دارد: اعداد می توانند در مجموعههایی گروهبندی شوند. همین. البته خود این گزاره را می توان به صورت خلاصه در آورد: اشیا را می توان در مجموعههایی گروهبندی کرد. می توانید اعداد 1، 2، 3 و 4 را در مجموعه {1، 2، 3، 4} قرار بدهید و آن را مجموعه «الف» نامگذاری کنید. حتی می توانید حرف «د»، ساندویچ ماهی، رمان توماس هاردی و سیاره نپتون را در مجموعه {«د»، ساندویچ ماهی، رمان توماس هاردی و سیاره نپتون} قرار دهید و آن را مجموعه «ب» بنامید.
خب لابد فکر می کنید این نظریه چیزی نیست که شما را تحت تاثیر قرار بدهد، اینطور نیست؟ اما نکته جالب توجه این است که ما فقط چند گام با آن نگرش بزرگ در راستای اِفشای بی نهایت فاصله داریم. حالا بگذارید فرض کنیم شما آن دو مجموعهای را که در بالا توصیف کردیم، با هم مقایسه می کنید. کدام یک بزرگتر است، مجموعه الف یا مجموعه ب؟ اگر در قالب عبارات فردی درباره آن فکر کنید، شاید یک تکلیف بی معنی بنظر برسد؛ برای مثال، چطور می توانید رمان توماس هاردی را با عدد ۳ مقایسه کنید؟ در اینجا، نکته کلیدی این نیست که به عبارات خاص نگاه کنید، بلکه باید به تعداد عبارات توجه کنید. چون چهار عبارت در هر دو مجموعه وجود دارد، آنها اندازه یکسانی دارند.
چطور استنباط کردیم که چهار عبارت در هر دو مجموعه وجود دارد؟ حدس می زنم اکثر شما به سادگی تعداد عباراتِ موجود در هر مجموعه را شمرده و سپس آنها را مقایسه کردهاید. اما بگذارید فرض کنیم شما هیچ چیزی درباره اعداد نمی دانستید و نحوه شمارش را بلد نبودید. در این صورت چطور می توانستید دو مجموعه را مقایسه کنید؟ خب این سوال قدری عجیب و غریب به نظر می آید، اما بخشی از آنچه نظریه مجموعه را جالب و قوی می کند این است که می تواند به طور کامل جدا از تمامی دیگر ریاضیات باشد؛ یعنی ما نیازمند راهی برای مقایسه مجموعهها بدون تکیه بر شمارش هستیم.
حتی اگر اصلا نمی دانستید چند عبارت در هر یک از آن دو مجموعه وجود دارد، همچنان مقایسه آنها می تواند کار سادهای باشد. فقط باید به مجموعه «الف» نگاه کنید و با عبارتی در مجموعه «ب» تطبیق دهید. شما باید این فرایند را تا آنجایی ادامه دهید که دیگر هیچ عبارتی در مجموعههای الف و ب باقی نمانده باشد. با رفتن از چپ به راست، می توانید ۱ را با «د»، ۲ را با «ساندویچ ماهی»، ۳ را با رمان «توماس هاردی» و ۴ را با «سیاره نپتون» جفت کنید. بدون نیاز به دانستن دقیق اینکه چند عبارت در هر مجموعه وجود دارد، می دانیم که دو مجموعه اندازه یکسانی دارند. این عامل با عنوان «تناظر یک به یک» شناخته می شود و این اجازه را به ما می دهد تا بدون نیاز به شمردن عبارات موجود در مجموعهها به مقایسه آنها بپردازیم. احتمالا می توانید ببینید که آن بخش آخر چگونه ما را به آستانه در بی نهایت می برد. تاکنون، فقط وانمود می کردیم که نمی توانیم تا چهار بشماریم، اما اگر مجموعهای با عبارات بی نهایت درست کنیم، چه می شود؟ مثالی که از قدیم وجود دارد این است که یک مجموعه حاوی اعداد طبیعی می باشد و همهشان اعداد صحیح غیرمنفی هستند که با صفر شروع می شود.
مفهوم ریاضی الف صفر
در الف صفر، مجموعهای داریم که به طور کلی از اعداد طبیعی تشکیل یافته است. حالا کدام یک بزرگتر است، الف صفر یا الف صفر ۱+؟ وقتی درباره بزرگترین اعداد متناهی حرف می زنیم، مفهوم «به اضافه ۱» همواره خود را نشان می دهد. با دلایل خوب، همواره می توانید ۱ را به عددی متناهی اضافه کرده و چیزی حتی بزرگتر بدست آورید. اما آیا این در خصوص الف صفر هم کارساز است؟ خب، بگذارید «ساندویچ ماهی» را از مجموعه خودمان قرض بگیریم و به مجموعۀ اعداد طبیعی اضافه کنیم؛ خب حالا مجموعهای با عبارات «الف صفر به اضافه ۱» داریم.
همانطور که ذکر شد، تنها راه مقایسه این دو مجموعه، استفاده از تناظر یک به یک است. ساندویچ ماهی را در آغاز یک مجموعه قرار می دهیم و مجموعه «پ» نامگذاری می کنیم، اما مجموعه «ت»، مجموعهای استاندارد از اعداد طبیعی خواهد بود. پس مجموعه «پ» عبارتست از {ساندویچ ماهی، ۰، ۱، ۲، ۳، ۴ …}، اما مجموعه «ت» عبارتست از {۰، ۱، ۲، ۳، ۴، ۵ …}. ما ساندویچ ماهی را با صفر، صفر را با ۱، ۱ را با ۲، ۲ را با ۳، ۳ را با ۴ و ۴ را با ۵ و … تطبیق خواهیم داد. هنوز عبارات بی نهایت در هر دو مجموعه وجود دارد و می توانیم بدون اینکه عبارتی کم بیاوریم، تا آنجا که دوست داریم از تناظر یک به یک بهره ببریم. یعنی الف صفر و الف صفر به اضافه ساندویچ ماهی دقیقا یکسان و برابر هستند.
این یک نتیجه واقعا عجیب و دور از عقل سلیم است. گئورگ کانتور این جمله مشهور را در هنگام بحث پیرامون ریاضی ماورای بی نهایت به زبان آورد: «آن را می بینم، ولی باورش نمی کنم.» و مسئله از این هم عجیبتر می شود. در اینجا یک سوال مطرح می شود؛ کدام مجموعه بزرگتر است، مجموعه اعداد طبیعی زوج یا مجموعهای که تمامی اعداد آن طبیعیاند؟ یک دیدگاه متناهی به ما می گوید که همه اعداد زوج و فرد باید دو برابر همه اعداد زوج باشند، اما تناظر یک به یک مشخص می کند که تا زمانی نظریه مجموعه در کار است، آن دو برابر هستند. وقتی بی نهایت را به ۲ ضرب می کنید، هنوز با بی نهایت روبرو هستید.
حالا اجازه دهید یک چالش جدی را مطرح کنیم. خب در مورد مجموعهای با اعداد تماما منطقی چه شرایطی حاکم است؟ یعنی تمام اعدادی که می توانند بعنوان کسری از دو عدد صحیح بیان شوند. ما درباره مجموعۀ بی نهایت بزرگ {…، ۵/۱، ۴/۱، ۳/۱، ۲/۱، ۱/۱} حرف می زنیم که مجموعه بی نهایت بزرگ {…، ۵/۲، ۴/۲، ۳/۲، ۲/۲، ۱/۲} و مجموعه بی نهایت بزرگ {…، ۵/۳، ۴/۳، ۳/۳، ۲/۳، ۱/۳} و غیره پس از آن مجموعه وجود دارند. ما در مورد مقداری بی نهایت از مجموعههای بی نهایت حرف می زنیم.
اگر قرار باشد چیزی ما را به عدد بی نهایت بزرگتری از الف صفر نزدیکتر کند، باید فقط به شیوه فوق عمل کرد، این طور نیست؟ می توانیم تناظر یک به یک را میان همه اعداد طبیعی و همه اعداد منطقی انجام دهیم، به طوری که ۱ صورت کسر باشد، اما همچنان کفایت نمی کند. ولی هنوز می توان یک تناظر یک به یک میان دو مجموعه تشکیل داد. برای اینکه نشان دهیم چطور می توان چنین کاری انجام داد، باید جدول سادهای درست کنیم. بگذارید تمامی اعداد منطقی را که در آن ۱ صورت کسر است، در ردیف اول قرار دهیم، همه اعداد منطقی با ۲ به عنوان صورت کسر در ردیف دوم قرار دهیم و این کار را تا زمانی انجام دهیم تا ستونها و ردیفهای بیشماری داشته باشیم:
۱/۱, ۱/۲, ۱/۳, ۱/۴, ۱/۵ …
۲/۱, ۲/۲, ۲/۳, ۲/۴, ۲/۵ …
۳/۱, ۳/۲, ۳/۳, ۳/۴, ۳/۵ …
۴/۱, ۴/۲, ۴/۳, ۴/۴, ۴/۵ …
۵/۱, ۵/۲, ۵/۳, ۵/۴, ۵/۵ …
…
خب می دانیم که جالب به نظر نمی رسد، اما در اینجا شاهد بخشهای آغازین یک جدول بی نهایت هستیم و همه اعداد منطقی ممکن در اینجا نمایان خواهند شد. این واقعیت که ما توانستهایم در هر صورت این جدول را بسازیم، اعلام می دارد که تناظر یک به یک امکانپذیر است، اما بگذارید ببینیم دقیقا چطور می توان این کار را انجام داد. در ابتدا، عدد طبیعی اول ۰ را با ۱/۱ تطبیق دهید. بعد، به قسمت پایین ستون بروید و ۱ را با ۱/۲ تطبیق بدهید. حالا به صورت مورب به بالا بروید و ۲ را با ۲/۱ تطبیق بدهید. سپس، به ستون اول بازگردید و ۳ را با ۱/۳ تطبیق دهید. در صورت حرکت به صورت مورب، ۴ با ۲/۲ و ۵ با ۳/۱ مطابقت پیدا می کند. می توانیم این کار را برای هر دو مجموعه به طور بی نهایت انجام داد. این واقعیت که سرعت حرکت ما در اعداد طبیعی بسیار سریع تر از اعداد منطقی است، اهمیت ندارد. آنچه اهمیت دارد این است که راهی برای آرایش اعداد منطقی در یک مجموعه بی نهایت پیدا کردهایم.(سایت بیگ بنگ، مقاله درآمدی مختصر بر مفهوم بی نهایت)
[10] بینهایت کوچکها، کمیتهایی هستند که بیش از هر عدد حقیقی استانداردی به صفر نزدیک اند ولی صفر نیستند. این اعداد در مجموعهٔ اعداد حقیقی معمول وجود ندارند ولی در سیستمهای عدد دیگر مثل اعداد سورئال و اعداد ابرحقیقی وجود دارد.(سایت ویکی پدیا)
تاریخچه مفهوم شگفت انگیز بی نهایت، از گذشته های دور ذهن ریاضی دانان را به خود مشغول کرده بود. هر چند برخی معتقدند که مفهوم بی نهایت برای نخستین بار در تمدن هند باستان مطرح شده است، اما می توان گفت که نخستین کار جدی در مورد بی نهایت در عرصه ریاضیات به دوران یونان باستان و تحقیقات اقلیدس بر روی اعداد اول باز می گردد. اقلیدس در کتاب مشهور ” اصول ” خود هر چند مستقیماً نامی از بی نهایت نمی برد، اما به طور ضمنی به آن اشاره می کند که ” بزرگترین عدد اول، از حاصل ضرب هر تعداد مفروضی از اعداد اول هم بزرگتر است “. پس از اقلیدس، پژوهش در مورد بی نهایت توسط سایر ریاضی دانان همچنان ادامه یافت تا سرانجام نماد ∞ به عنوان نماد ابن مفهوم اسرارآمیز پا به عرصه ریاضیات گذاشت. با آغاز عصر جدید، پژوهش در مورد بی نهایت همچنان ادامه یافت. در این دوران ” گاتفرید ویلهلم لایبنیتز” و ” ایزاک نیوتن ” برای نخستین بار از وجود مفهوم جدیدی به نام ” بی نهایت کوچک ” در عرصه ریاضیات پرده برداشتند. بی نهایت کوچک که عملا از همان مفهوم بی نهایت مشتق شده است، عددی مثبت است که از هر عدد مثبت مفروض دیگری کوچکتر است. بدین ترتیب ” بی نهایت ” به همراه پسر عموی کوچک خود یعنی بی نهایت کوچک، پایه های عرصه بدیعی از ریاضیات به نام ” حساب دیفرانسیل و انتگرال ” ( حسابان) را شکل دادند و ابن گونه بود که بی نهایت عملا به مهمترین مفهوم در علوم و مهندسی جدید تبدیل شد.(سایت بیگ بنگ، مقاله کانتور و اسرار بی نهایت)
کمیت های بینهایت کوچک یا infinitesimals تاریخ پر فراز و نشیبی در ریاضیات داشته اند. استفاده از این مفهوم در طی قرون ۱۲ تا ۱۶ میلادی در میان ریاضیدانان هندی معمول بوده است. به هنگام اولین مراحل توسعه حساب دیفرانسیل و انتگرال در قرن هفدهم، ریاضیدانانی همچون لایبنیتز برای توضیح و تسهیل انجام عملیاتی که اکنون با عنوان فرایند حدگیری شناخته می شود، آزادانه از آنها استفاده می کردند.
استعمال این مفاهیم به گونه ای غیر رسمی انجام می گرفت و اگرچه به نظر می رسید که این استعمال بر مبنای یک درک شهودی قوی صورت می گیرد، با این حال احساس شد که مباحث مرتبط با کمیت های بینهایت کوچک حتی می تواند منجر به نتایج نادرست گردد. لذا این کمیت ها در نظر ریاضیدانان مبدل به چیزهایی نامطلوب شدند و این در حالی بود که همچنان، اگرچه به طور غیر سیستماتیک، مورد استفاده فیزیکدانان و مهندسان قرار داشتند. حتی ادعا شد که ایده یک کمیت بینهایت کوچک ذاتا با خودش در تناقض است.این ادعای اخیر کاملا بی مورد است. آنچه حقیقتا می توانست گفته شود این بود که دستگاه های کلاسیک اعداد ( همچون مجموعه اعداد گویا ) که در آنالیز مورد استفاده قرار می گیرند دارای عنصر بینهایت کوچکی غیر از صفر نیستند. همواره این بحث مطرح بوده است که آیا دستگاه اعداد مفیدی می توان یافت که کمیت های بینهایت کوچک را نیز داشته باشد؟
لایبنیتز معتقد بود که باید این امکان وجود داشته باشد که دستگاهی از اعداد ساخته شود که هم شامل کمیت های بسیار بزرگ است و هم کمیت های بسیار کوچک را در بر دارد و در عین حال همان مناسباتی که در بین اعداد معمولی وجود دارد در این دستگاه نیز برقرار باشد. اما تقریبا بلافاصله انتقاداتی جدی نسبت به استفاده از مفهوم بینهایت کوچک مطرح شد و تلاشهایی صورت گرفت تا حساب دیفرانسیل و انتگرال بر مبنایی که عمیقا بتوان به آن متکی بود شکل گیرد. بالاخره در قرن نوزدهم وایراشتراس نظام کاملا سختگیرانه و منطقی را پدید آورد که به شدت بر پایه دستگاه اعداد حقیقی ( که همانطوری که می دانیم دارای خاصیت ارشمیدسی است و لذا عنصر بینهایت کوچک غیر صفر ندارد ) و آنچه که امروزه تحت عنوان تعریف حد( با اپسیلن و دلتا ) شناخته می شود استوار بود.
اما در دهه ۱۹۶۰ Abraham Robinson دریافت که مفهومی وجود دارد که برنامه اولیه لایبنیتز می تواند به طور کاملا منطقی بر مبنای آن صورت گیرد. اشارات و موارد استفاده از آنچه که امروزه آنالیز غیر استاندارد نام گرفته است بسیار فراتر است از استفاده خاص در حساب دیفرانسیل که مد نظر لایبنیتز بود.
[11] ملاصدرا در بیان اقسام بی نهایت و تفکیک بین بی نهایت بالقوة و بی نهایت بالفعل می فرماید:
و منها أن غير المتناهي على معنيين: أحدهما بالقوة و هو غير المتناهي اللايقفي
و ثانيهما بالفعل و هو غير المتناهي العددي، و مقدورات الله تعالى عند المتكلمين غير متناهية بالمعنى الأول لا بالمعنى الثاني لأنهم منكرون لوجود الغير المتناهي بالفعل مرتبا كان أو غير مرتب متعاقبا كان أو مجتمعا و التفاوت إنما يجوز في غير المتناهي بالمعنى الأول كقبول الجسم عند الحكماء للأنصاف المتداخلة غير المتناهية و الأرباع المتداخلة غير المتناهية و الثانية نصف الأولى.(الحکمة المتعالیة، ج ٧، ص ٣١٨)
شهید مطهری بی نهایت بالقوة را این گونه تبیین می کند:
اعداد متناهى نيستند؛ يعنى اگر اعداد را بيان كرده و بالا برويم و بگوييم ۱، ۲، ۳،…، ۱۰۰۰،…، ۱۰۰۰۰۰۰،… هر چه بالا برويم به عددى كه ما فوق آن نتوان عددى را فرض كرد نمىرسيم. هر عددى را كه ما فرض كنيم باز هم ما فوق آن عددى فرض مىشود، بلكه براى آن عدد دو برابر هم فرض مىشود، بلكه خودش ضرب در خودش هم فرض مىشود، خود آن به قوۀ ۲ و ۳ و ۴ و ۵ و… هم فرض مىشود. هر عددى را كه شما اعتبار كنيد و بگوييد اين آخرين عدد است باز هم بالاتر از آن عدد است. اين است كه مىگويند اعداد غير متناهى است.
امّا اينكه مىگويند اعداد غير متناهى است، منظور غير متناهى بالفعل نيست، بلكه منظور «غير متناهى لا يقفى» است. لايتناهى بالفعل يعنى اينكه ما يك موجود بالفعل غير متناهى داشته باشيم، مثل اينكه كسى بگويد ستارههاى عالم بالفعل غير متناهىاند، ذرّات عالم بالفعل غير متناهىاند؛ كه اگر كسى گفت ستارهها بالفعل غير متناهى است، بايد بگوييم ما الآن غير متناهى عدد ستاره در خارج داريم. اين يك مسأله است. امّا آنكه مىگويد عدد غير متناهى است، به اين معنا نمىگويد. منظور غير متناهى لا يقفى است. غير متناهى لا يقفى به ذهن ما برمىگردد، به خارج مربوط نيست؛ يعنى ذهن ما هر عددى را كه اعتبار كند عدد در آنجا متوقف نمىگردد؛ امكان اعتبار عددى ديگر كه يكى بيشتر يا دوتا بيشتر يا دو برابر آن يا هزار برابر آن باشد هست. اين را مىگويند «لا يتناهى لا يقفى». شيخ همين جا اشكال خود را وارد مىكند.(مجموعه آثار شهید مطهری، ج ٧، ص ۵۶٧-۵۶٨)
تناهى به دو معناست: يكى تناهى عددى، و ديگر تناهى لا يقفى.
نامتناهى عددى آن است كه شىء بالفعل موجود و نامتناهى باشد، مثلا خط و سطح و جسم بالفعل موجود باشد و نهايت نداشته باشد. و نامتناهى لا يقفى آن است كه بالفعل موجود نباشد، بلكه به هر مرتبه كه رسد باز در آن چيزى بتوان فرض نمود.چنانچه حكما گويند كه جسم قابل قسمت است الى غير النهاية، كه هر اندازه جسم را تقسيم كنيم باز هم قابل قسمت است و به انتهاء نمىرسد. و اينكه حكما گويند نامتناهى وجود ندارد مقصود نامتناهى عددى است، ولى نامتناهى لايقفى جائز و واقع است، مثل اينكه جسم به نامتناهى تقسيم مىشود و اين قسمتها به جايى نمىرسند كه ديگر تقسيم نشوند. حكماى قديم يونان مىگفتند ابعاد نامتناهى است.(مجموعه رسائل عرفانی و فلسفی،ص ٢۶٩)
این اصطلاح اولین بار در کلام ارسطو به کار رفته است. او در این باره می گوید:
قال الإسكندر: هل المتحرك على عظم ما يتحرك فى أول حركته على أول جزء منه، أم لا؟ و ذلك أن كل حركة إنما صارت فى زمان لأنه ليس يمكن أن يتحرك المتحرك على الشىء الموضوع ليتحرك عليه دفعة، لكنه يقطع منه شيئا بعد شىء؛ فإذا هذا هكذا، فالمتحرك يتحرك أولا على أول جزء من أجزاء العظم الذي يتحرك عليه. فإن كان الأول فى العظم يمر بلا نهاية، فكل محرك يصير متحركا على أشياء بلا نهاية؛ و كل متحرك يتحرك بعدا ما، فإنه يكون متحركا آخرا بلا نهاية أولية. و الأشياء التي بلا نهاية لا تقطع مسافتها، فنقول: إنه لا بد – إذ كانت قسمة الأشياء المتصلة بلا نهاية – من أحد أمرين: إما أن تكون الحركة لا تجوز أولا على الجزء الأول، أو تكون قد تجوز على الجزء الأول من العظم إنما هو من قبل أن فى العظم المتصل جزءا يتقدم و جزءا يتأخر. و ذلك أنه ليس الأجزاء فى المتصل بحال غير الحال التي نقول بها إن المتحرك نفسه يقطعها؛ فكيف إذا يوجد بعض الأجزاء متقدما و بعضها متأخرا فى المتصل، إما بالفعل أم بغير الفعل؟ فنقول: إنه ليس شىء من الأعظام المتصلة أجزاؤه منفصلة، و لا هى فى الكل بالفعل، لأن العظم إنما هو غير منقسم بالفعل؛ و لو كان منقسما بالفعل، لما كان عظما واحدا، و لا كانت الحركة واحدة. فإذ كانت الأجزاء التي فى الكل ليست بالفعل فيه فقد بقى أن يكون فى الكل الذي هو متصل بالقوة، و يكون المتقدم و المتأخر المتصل إنما هو بالقوة لا بالفعل، و يكون المتحرك عليه إنما يتحرك على الجزء الأول أولا على الحال التي يوجد بها الجزء فى العظم، و وجوده فيه بالقوة. فعلى هذه الجهة إذا يتحرك عليه. و إنما يفعل هذا من قبل أنه يتحرك عليه من غير أن يقسمه و من غير أن يجعل جزءا منه أولا و جزءا ثانيا بالفعل. و المتحرك إذا تحرك على هذه الجهة على العظم فإنما يكون متحركا فى الأجزاء الأوائل على حسب ما هى فى العظم بلا نهاية، و وجودها فى العظم بلا نهاية إنما هو بالقوة. و معنى قولنا: إنه غير متناهية القوة، لا تقطع مسافتها؛ بل إنما وضعنا ذلك فيما كان بالفعل.( أرسطو عند العرب، صفحه: ۲۷۸)
او در جای دیگر در مورد بی نهایت های بزرگ(در اعداد) و کوچک(در مقادیر) چنین می نویسد:
و بالواجب أيضا لزم أن يكون غير المتناهى أمّا بالزيادة فقد يظن أنه لا يمكن أن يتجاوز كل مقدار، و أما بالقسمة فقد يمكن؛ و ذلك أن <غير المتناهى و> الهيولى محاط بهماداخلا، و هى الشىء غير المتناهى و المحيط هو الصورة. و بالواجب أيضا صار فى العدد فى الذهاب إلى القلة نهاية، و فى الذهاب إلى الكثرة يزيد أبدا على كل عدة. و صار فى المقدار الأمر بالضد: أما إلى الصغر فقد يتجاوز كل مقدار، و أما إلى الكبر فلا يمكن أن يوجد مقدار غير متناه. و السبب فى ذلك أن الواحد غير منقسم – أىّ واحد كان – مثل الإنسان إنه إنسان واحد لا كثير، و العدد إنما هو آحاد كثيرة و كمية ما. فقد يجب أن نقف عند ما لا ينقسم، فإن الاثنين و الثلاثة إنما هى أسماء، و كذلك واحد من سائر الأعداد. و أما ذهابه إلى الكثرة فقد يمكن توهمه دائما. فإن قسمة المقدار بنصفين، و نصفه بنصفين يمر بلا نهاية، فيكون <العدد غير متناه> بالقوة ؛ فأما بالفعل – فلا. غير أنه قد يوجد منه ما يزيد دائما على كل عدة محددة، لكن هذا العدد ليس بمفارق لهذه القسمة، و لا بلا نهاية أمر باق، لكنه أمر يتكون دائما، و كذلك الزمان و عدد الزمان.
فأما المقادير فإن الأمر فيها بالضد، و ذلك أن المتصل قد ينقسم بلا نهاية؛ غير أنه فى العظم ليس يكون غير متناه. لأنه بأىّ مقدار كان يمكن أن يكون بالقوة، فإنه بذلك المقدار يمكن أن يكون بالفعل. فإذ ليس يوجد أصلا مقدار محسوس غير متناه، فليس يمكن أن يكون يفضل على كل مقدار محدود، لأن ذلك لو جاز لقد كان سيكون ما هو أعظم من السماء.( الطبیعة (أرسطو)، جلد: ۱، صفحه: ۲۶۳)
در کلمات سایرین:
و الجواب: أنّ لا نهاية إمكان القسمة خاصّة للأجسام كلّها. و كما لا يلزم من اشتراك الكلّ و الجزء في الجسميّة اشتراكهما في خصوص المقدار، كذلك لا يلزم من اشتراكهما في خاصّة الجسم، و هي لا نهاية إمكان القسمة، اشتراكهما في خصوص المقدار. سلّمنا أنّ الشيئين إذا اشتركا في عدم التناهي اشتركا في عدم التفاوت، و لكن لا مطلقا، بل فيما يكون أعدادهما الغير المتناهية حاصلة بالفعل. أمّا إذا كانت بالقوّة فلا، كيف و الوجود يكذّبه.
ألا ترى أنّ الألوف المتضاعفة إلى غير النهاية بالقوّة و الإمكان فيها من المئات الغير المتناهية بالقوّة عشرة أمثالها، و من العشرات مائة أمثالها، مع أنّ عدد كلّ عقد من الثلاثة غير متناه بالقوّة؛ بمعنى أنّا إلى أيّ حدّ انتهينا في العدد أمكن الزّيادة عليه؛ لكن لمّا لم تكن هذه الألوف الغير المتناهية حاصلة بالفعل، لم يلزم من الاشتراك في اللاّنهاية التساوي في الأعداد(حکمة الإشراق (تعلیقه ملا صدرا)، جلد: ۱، صفحه: ۳۲۲)
السادس أن العدد ليس بمتناه و معناه أنه لا توجد مرتبة من العدد إلا و يمكن فرض ما يزيد عليها و كذا فرض ما يزد على الزائد و لا تقف السلسلة حتى تنقطع بانقطاع الاعتبار و يسمى غير المتناهي اللايقفي و لا يوجد من السلسلة دائما بالفعل إلا مقدار متناه و ما يزيد عليه فهو في القوة و أما ذهاب السلسلة بالفعل إلى غير النهاية على نحو العدول دون السلب التحصيلي فغير معقول فلا كل و لا مجموع لغير المتناهي بهذا المعنى و لا تحقق فيه لشيء من النسب الكسرية كالنصف و الثلث و الربع و إلا عاد متناهيا .(نهایة الحکمة، ص ١١٢-١١٣)
[12] آنالیز، آنالس به انگلیسی: (Analysis)، واکافت، واکاوی یا تجزیه و تحلیل شکستن یک مجموعه به بخشهای کوچک برای فهم بهتر آن است. به عبارت دیگر، آنالیز، تجزیه و تحلیل دادهها برای گرفتن نتیجهٔ پیچیدهتر نیز میتواند باشد.
در دانش شیمی، آنالیز به تجزیه نمونه و بررسی آن اطلاق میشود که در شاخه شیمی تجزیه دنبال میگردد. در دانش ریاضیات و آمار، آنالیز به بررسی احتمالات و ریزحالتها میپردازد.(سایت ویکی پدیا، مدخل آنالیز)
آنالیز ریاضی بخشی از ریاضیات است که با مفاهیم حد و همگرایی سروکار دارد و در آن موضوعاتی مثل پیوستگی و انتگرالگیری و مشتقپذیری و توابع غیرجبری بررسی میشود. این موضوعات را معمولاً در عرصهٔ اعداد حقیقی یا اعداد مختلط و توابع مربوط به آنها بحث میکنند ولی میتوان آنها را در هر فضائی از موجودات ریاضی که در آن مفهوم «نزدیکی» (فضای توپولوژیک) یا «فاصله» (فضای متریک) وجود دارد به کار برد. آنالیز ریاضی از کوششهای مربوط به دقیق کردن مبانی و تعریفهای حسابان سر برآورده است.
آنالیز ریاضی دارای چندین زیرشاخه به این شرح است:
آنالیز حقیقی
آنالیز مختلط
آنالیز عددی
آنالیز تابعی
آنالیز هارمونیک
آنالیز غیراستاندارد (سایت ویکی پدیا، مدخل آنالیز ریاضی)
آنالیز شاخه ای از ریاضیات است که با اعداد حقیقی و اعداد مختلط و نیز توابع حقیقی و مختلط سر و کار دارد و به بررسی مفاهیمی از قبیل پیوستگی، انتگرال گیری و مشق پذیری می پردازد. از نظر تاریخی آنالیز در قرن هفدهم با ابداع حساب دیفرانسیل و انتگرال توسط نیوتن و لایپ نیتس پایه ریزی شد. در قرن هفدهم و هجدهم سر فصل های آنالیزی از قبیل حساب تغییرات، معادلات دیفرانسیل با مشتقات جزئی، آنالیز فوریه در زمینه های کاربردی توسعه فراوانی یافتند و از آنها به طور موفقیت آمیز در زمینه های صنعتی استفاده شد. در قرن هجدهم تعریف مفهوم تابع به یک موضوع بحث بر انگیز در ریاضیات تبدیل شد.
در قرن نوزدهم کوشی با معرفی مفهوم سری های کوشی اولین کسی بود که حساب دیفرانسیل و انتگرال را بر یک پایه منطقی استوار کرد. در اواسط قرن نوزدهم ریمان تئوری انتگرال گیری خود را که به انتگرال ریمان معروف است ارائه داد، در اواخر قرن نوزدهم وایراشتراس مفهوم حد را معرفی کرد و نتایج کار خود بر روی سریها را نیز ارائه داد، در همین دوران ریاضیدانان با تلاش های زیاد توانستند انتگرال ریمان را اصلاح نمایند.
در اوایل قرن بیستم هیلبرت برای حل معادلات انتگرال فضای هیلبرتی را تعریف و معرفی نمود. از آخرین تحولات در زمینه آنالیز می توان به پایه گذاری آنالیز تابعی توسط یک دانشمند لهستانی به نام باناچ نام برد .
آنالیز به دسته های زیر تقسیم بندی می شود :
آنالیز حقیقی: به مطالعه بر روی حد ها، مشتقات، انتگرال ها سریهای توانی می پردازد
آنالیز تابعی: به معرفی نظریه هایی از قبیل فضاهای باناچ و نیز فضای هیلبرت می پردازد
آنالیز هارمونیک: در این شاخه از آنالیز سری های فوریه مورد مطالعه قرار می گیرد
آنالیز مختلط: به بررسی توابع مختلط و خواص این توابع از قبیل مشتق پذیری و انتگرال گیری می پردازد
آنالیز عددی: آنالیز عددی الگوریتم حل مسئله در ریاضیات پیوسته(ریاضیاتی که جدا از ریاضیات گسسته است) را مورد مطالعه قرار میدهد.
آنالیز عددی اساسا به مسائل مربوط به متغیرهای حقیقی و متغیرهای مختلط و نیز جبر خطی عددی به علاوه حل معادلات دیفرانسیل و دیگر مسائلی که از فیزیک و مهندسی مشتق میشود. تعدادی از مسائل در ریاضیات پیوسته دقیقا با یک الگوریتم حل میشوند. که به روش های مستقیم حل مسئله معروف اند. برای مثال روش حذف گائوسی برای حل دستگاه معادلات خطی است و نیز روش سیمپلکس در برنامه ریزی خطی مورد استفاده قرار میگیرد. ولی روش مستقیم برای حل خیلی از مسائل وجود ندارد و ممکن است از روشهای دیگر مانند روش تکرارشونده استفاده شود، چون این روش میتواند در یافتن جواب مسئله موثرتر باشد.
تخمین خطاهای موجود در حل مسائل از مهمترین قسمت های آنالیز عددی است این خطاها در روش های تکرار شونده وجود دارد چون به هرحال جوابهای تقریبی بدست آمده با جواب دقیق مسئله، اختلاف دارد و یا وقتی که از روش های مستقیم برای حل مسئله استفاده می شود خطاهایی ناشی از گرد کردن اعداد بوجود می آید. در آنالیز عددی می توان مقدار خطا را در خور روش که برای حل مسئله به کار می رود، تخمین زد. الگوریتم های موجود در آنالیز عددی برای حل بسیاری از مسائل موجود در علوم پایه و رشته های مهندسی مورد استفاده قرار می گیرند. برای مثال از این الگوریتم ها در طراحی بناهایی مانند پل ها، در طراحی هواپیما ، در پیش بینی آب و هوا، تهیه نقشه های جوی از زمین، تجزیه و تحلیل ساختار مولکول ها، پیدا کردن مخازن نفت، استفاده می شود، همچنین اکثر ابر رایانه ها به طور مداوم بر اساس الگوریتم های آنالیز عددی برنامه ریزی می شوند. به طور کلی آنالیز عددی از نتایج عملی حاصل از اجرای محاسبات برای پیدا کردن روش های جدید برای تجزیه و تحلیل مسائل، استفاده میکند.(وبلاگ ریاضی ریاضی است، مقاله آنالیز ریاضی)
[13] اشاره به مقاله «سه برهان تنبیهی بر مبرهن البرهان»
[14] افاده شده در جلسه سوم تاریخ و مباحث ریاضیات
[15] عدد پی (π) (به انگلیسی: Pi) از عددهای ثابت ریاضی و تقریباً برابر با ۳٫۱۴ است. این عدد را با علامت π نشان میدهند. عدد پی عددی حقیقی و گُنگ است که نسبت محیط دایره به قطر آن را در هندسهٔ اقلیدسی مشخص میکند و کاربردهای فراوانی در ریاضیات، فیزیک و مهندسی دارد. عدد پی همچنین به ثابت ارشمیدس نیز معروف است .پی،حرف اول کلمهٔ یونانی «پریمتروس» (به معنی محیط) است.(سایت ویکی پدیا)
[16] گشتن بهمعنای دور زدن و نه بهمعنای شدن
[18] پویانمایی نسبت عدد پی به دایره را در سایت ویکی پدیا مشاهده نمایید.
[19] افاده شده در جلسه هشتم فقه هوش مصنوعی تاریخ 2/ 9/ 1402
ارشمیدس محیط دایره را نمیدانست؛ اما ناامید نشد و از آنچه میدانست یعنی محیط یک مربع آغاز کرد. البته او در واقع با یک ششضلعی محاسبه خود را آغاز کرد؛ اما از آنجا که ترسیم و کار کردن با مربع آسانتر است، ما از مربع استفاده میکنیم.
ما محیط یک دایره را نمیدانیم؛ اما میتوانیم آن را بین دو مربع[محیطی و محاطی] رسم کنیم:

دقت کنید که این وضعیت شبیه مسیر مسابقهای با یالهای داخلی و خارجی است. محیط دایره هر چه که باشد بین محیط دو مربع قرار دارد، یعنی بیشتر از محیط مربع داخلی و کمتر از محیط مربع بیرونی است.محیط مربعها را میتوانیم به سادگی محاسبه کنیم:ما نمیدانیم که پی چقدر است؛ اما میدانیم که عددی بین 2.8 و 4 است. اگر تصور کنیم دقیقاً نیمه این دو کرانه باشد، پس باید در حدود 3.4 باشد.
مربعها گوشهدار هستند. آنها را نمیتوان چندان شبیه دایره دانست و این اختلاف موجب محاسبات نادرست و با اشتباه زیاد میشود؛ اما با افزایش اضلاع، برای مثال با استفاده از هشتضلعی میتوانیم حدس بهتری از عدد پی داشته باشیم.

نان که میبینید با افزایش تعداد اضلاع، به شکل یک دایره نزدیکتر میشویم. متأسفانه اعداد اعشاری در سال 250 قبل از میلاد هنوز اختراع نشده بودند، چه برسد به نرمافزارهای صفحه گسترده. بنابراین ارشمیدس مجبور بود که این فرمولها را به کمک کسرها حل کند. او کار خود را با ششضلعی آغاز کرد و با ١٢، 24، 48 و 96 ضلع ادامه داد. تخمین نهایی وی از عدد پی با استفاده از شکلی با 96 ضلع به صورت زیر بود:
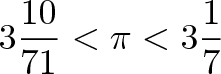
نقطه میانی این بازه برابر با 3.14185 است که تقریباً 99.9% دقیق است!(سایت فرادرس،مقاله عدد پی چگونه کشف شد؟)
[21] حد (به انگلیسی🙁 Limit): وقتی که مقادیر متوالی به یک متغیر نسبت داده میشود، و آن متغیر بینهایت به عدد ثابتی نزدیک شود، به طوری که اختلاف آنها از مقدار ثابت به هر اندازه کوچک قابل انتخاب باشد، این مقدار ثابت را حد همه مقادیر متغیر میگویند.(سایت ویکی پدیا)
[22] عدد غیر نسبی، گُنگ یا اصم به انگلیسی🙁 Irrational number) در دستگاه اعداد بهصورت عددی حقیقی تعریف میشود که عدد نسبی (عدد گویا) نباشد، یعنی نتوان آن را به صورت کسری نوشت که صورت و مخرجش عدد صحیح باشند.(همان)
عددی که جبری نباشد، عدد متعالی یا ترافرازنده یا غیرجبری نامیده میشود.
نمونههای برجستهای از اعداد ترافرازنده π و e میباشند. نمونههای کمی از اعداد ترافرازنده شناخته شدهاند چرا که اثبات ترافرازنده بودن یک عدد دشوار است. با این حال، شمار آنها کم نیست و تقریباً همهٔ اعداد مختلط و حقیقی ترافرازنده شمرده میشوند.
نخستین اثبات وجود اعداد ترافرازنده (متعالی) را جوزف لیوویل، ریاضیدان فرانسوی، در سال ۱۸۴۴ داده است.
(سایت ویکی پدیا، مدخل اعداد متعالی در این صفحه همچنین طبقه بندی اعداد را می توانید مشاهده کنید.)
اعداد گنگ دو نوع دارند: اعداد جبری (algebraic numbers) و اعداد متعالی (transcendental numbers)
مجموعه اعداد گنگ (Irrational Numbers)
به یک معنا، اعداد گنگ یک نوع خیلی فراگیر می باشند، هر عددی در خط اعداد که یک عدد گویا نباشد، یک عدد گنگ است.
با این تعریف، هیچ عدد گنگی نمی تواند به صورت کسری نمایش داده شود، همچنین یک عدد گنگ نمی تواند به شکل یک عدد اعشاری مختوم (terminating decimal) یا به شکل یک عدد اعشاری متناوب (repeating decimal) نمایش داده شود. (برای اطلاعات بیشتر در مورد این انواع اعداد اعشاری، فصل 11 را ببینید).
در عوض، یک عدد گنگ می تواند تقریبی از یک عدد اعشاری نامتناهی (non-terminating)، و غیر تکرار شونده (non-repeating) باشد:
یک رشته از اعداد بعد از ممیز اعشاری که بدون ایجاد یک الگو می توانند تا ابد ادامه پیدا کنند.
مشهورترین مثال از اعداد گنگ عدد پی (π) می باشد، که نماینده محیط یک دایره با قطر 1 واحد می باشد. یک عدد گنگ رایج دیگر 2√ می باشد، که نماینده طول قطر یک مربع با اندازه ضلع 1 واحد می باشد. در واقع، تمامی ریشه های توان دوم (square roots) از اعداد غیر مربع (non-square numbers) – مانند 3√، 5√، و به همین ترتیب – اعداد گنگ می باشند.
اعداد گنگ فضاهای موجود در خط اعداد حقیقی (real number line) را پر می کنند. (خط اعداد حقیقی همین خط اعدادی است که شما استفاده می کنید، اما متوالی است، هیچ جای خالی در آن وجود ندارد بنابراین هر نقطه ای بر روی آن با یک عدد جفت شده است.) اعداد گنگ در بسیاری از موارد که در آن نیاز به سطح دقت خیلی بالایی ندارید به شکل اعداد گویا مورد استفاده قرار می گیرند، اما مقدار دقیق آن عدد نمی تواند به صورت یک کسر نمایش داده شود.
اعداد گنگ دو نوع دارند: اعداد جبری (algebraic numbers) و اعداد متعالی (transcendental numbers). در مورد این دو نوع در ادامه همین فصل توضیحاتی را خواهم داد.
مجموعه اعداد جبری (Algebraic Numbers)
برای درک اعداد جبری، نیاز به اندکی دانش در مورد معادلات چند جمله ای (polynomial equations) دارید. یک معادله چند جمله ای، یک معادله جبری است که مطابق شرایط زیر باشد:
عملیات های آن محدود به جمع، تفریق، و ضرب باشد. به عبارت دیگر، لازم نیست که بر یک متغیر تقسیم کنید.
متغیرهای آن تنها به توان اعداد مثبت که در مجموعه اعداد کامل (whole-number) باشند، رسیده است.
شما می توانید در کتاب Algebra For Dummies اطلاعات بیشتری در مورد چندجمله ای ها بدست آورید.
در اینجا چند معادله چند جمله ای می بینید:
هر عدد جبری به عنوان راه حل حداقل یک معادله چند جمله ای، نشان داده می شود. برای مثال، فرض کنید معادله زیر را دارید:
شما می توانید این معادله را به شکل زیر حل کنید:
بنابراین 2√ یک عدد جبری می باشد که مقدار تقریبی آن برابر با …1.4142135623 است.
مجموعه اعداد متعالی (Transcendental Numbers)
یک عدد متعالی (transcendental number)، در مقایسه با یک عدد جبری، هرگز راه حل یک معادله چند جمله ای نمی باشد. مشابه اعداد گنگ، اعداد متعالی نیز یک نوع فراگیر هستند: هر عددی در خط اعداد که عددی جبری نباشد، یک عدد متعالی است.
مشهورترین عدد متعالی π می باشد، که مقدار تقریبی آن برابر با …3.1415926535 است. استفاده از این عدد در هندسه آغاز شد اما تقریباً به تمامی نواحی ریاضی گسترش یافت.
سایر اعداد متعالی مهم در هنگام مطالعه مثلثاث (trigonometry) برایتان پیش می آیند. سینوس ها (Sines) ، کسینوس ها (cosines)، تانژانتها (tangents) و سایر توابع مثلثاتی معمولاً اعداد متعالی می باشند.
یکی دیگر از اعداد متعالی مهم عدد e می باشد، که مقدار تقریبی آن …2.7182818285 است. عدد e مبنای لگاریتم طبیعی (natural logarithm) می باشد، که احتمالاً تا زمانی که وارد مبحث حساب دیفرانسیل و انتگرال (calculus) نشوید، از آن استفاده نخواهید کرد. مردم از e برای حل مسائل مربوط به بهره مرکب (compound interest)، رشد جمعیت (population growth)، فروپاشی رادیو اکتیو (radioactive decay)، و مواردی از این دست، استفاده می کنند.(سایت خوشآموز،مقاله ده مجموعه مهم اعداد که باید بشناسید)
[24] در جبر و هندسه، عددی حقیقی r عدد ترسیمپذیر (انگلیسی: Constructible number) است اگر و تنها اگر بتوان با داشتن پارهخط واحد، با خطکش و پرگار بتوان در تعداد مراحل متناهی پارهخطی به طول |r| رسم کرد. تمام اعداد حقیقی ترسیمپذیر نیستند و برای توصیف آنهایی که ترسیمپذیر هستند باید از روشهای جبری استفاده کرد.
یک نقطه در فضای دوبعدی ترسیمپذیر است اگر نقطهٔ پایانی پارهخط واحد باشد، یا نقطهٔ تقاطع دو خط که با نقاط ترسیمپذیر تعریف شدهاند، یا تقاطع خط و دایرهای که مرکزش نقطهای تقسیمپذیر باشد و از یک نقطهٔ تقسیمپذیر بگذرد، یا تقاطع دو تا از این دایرهها.
بهعبارت جبری، یک عدد ترسیمپذیر است اگر و تنها اگر بتوان آن را با اعمال مراحل متناهی چهار عمل اصلی و ریشه دوم (فقط ریشهٔ دوم و نه ریشههای بالاتر) بر اعداد ترسیمپذیر دیگر ساخت، و ۰ و ۱ بنابر تعریف تفسیر پذیرند.(سایت ویکی پدیا، مدخل عدد ترسیم پذیر)
عدد a را «رسم پذیر» گوییم اگر بتوان تنها با استفاده از خط کش و پرگار پاره خطی به طول a رسم کرد. و البته فرض ما بر این است که یک واحد طول داده شده باشد.از این به بعد هر جا کلمه رسم پذیری آمد منظور همان، رسم پذیری به وسیله خط کش و پرگار است.رسم پذیری بعضی عددها بسیار واضح است. مثلا ۱ و ۲ و … اما بعضی دیگر احتیاج به بررسی دارند مثل 2√ . آیا این عدد رسم پذیر است؟
از دوران دبیرستان به یاد داریم که : از هر نقطه خارج یک خط مفروض می توان خطی عمود بر آن رسم کرد.اگر محل تلاقی این دو خط را مبدأ،در نظر بگیریم به این محور، محور رسم پذیر می گوییم.
در این محور:
۱(a,0)يا(0,a) را رسم پذیر گوییم اگر a رسم پذیر باشد.
۲) (a,b) را رسم پذیر گوییم اگر a و b رسم پذیر باشند.
هر شکلی را که روی این محور بتوان رسم کرد، اعم از پاره خط، دایره و… یک شکل رسم پذیر گوییم.
حال می توانیم به راحتی بگوییم که 2√رسم پذیر است. چون اگر(۰.۱)و (۰و۱) را روی محور به هم وصل کنیم بنابر قضیه فیثاغورث پاره خطی به طول 2√داریم. حال سوالی که مطرح می شود این است که آیا همه اعداد رسم پذیرند؟ و اگر نه چه عددهایی رسم پذیرند و کدام ها رسم پذیر نیستند. همه عددها رسم پذیر نیستند و تعیین رسم پذیری آنها به کارهای تخصصی میانجامد.
حال سوالی که مطرح می شود این است که آیا همه اعداد رسم پذیرند؟ و اگر نه چه عددهایی رسم پذیرند و کدام ها رسم پذیر نیستند. همه عددها رسم پذیر نیستند و تعیین رسم پذیری آنها به کارهای تخصصی می انجامد اما حالا که مفهوم عدد رسم پذیر رو فهمیدیم چند حکم کلی درباره رسم پذیری رو هم بیان می کنیم:
۱) اگر a و b رسم پذیر باشند آنگاه a+b , a b , a.b , a/b نیز رسم پذیرند.
۲) اگر a رسم پذیر باشد آنگاه رادیکال a نیز رسم پذیر است.
۳) موارد زیر معادلند (یعنی اگر یکی از آنها در مورد یک عدد درست باشد دو تای دیگر نیز درستند):
الف) x رسم پذیر است.
ب) (Cos(x رسم پذیر است.
ج) (Sin(x رسم پذیر است.
۴) همه اعداد گویا (Q) رسم پذیر هستند.
اکنون کار قضاوت در مورد رسم پذیری عددها خیلی ساده تر شد. تنها عددی ممکن است رسم پذیر نباشد که گنگ باشد. اما تعیین اینکه عدد گنگی رسم پذیر است یا نه دارای تکنیکهای ویژه ایست.
.(سایت آی هوش، مقاله رسم پذیر بودن یک عدد)
[26] در سال ۱۷۶۱ لامبرت ریاضیدان سوئیسی ثابت کرد که عدد پی گنگ است و نمیتوان آن را به صورت نسبت دو عدد صحیح نوشت. همچنین در سال ۱۸۸۲ فردیناند فون لیندمان ثابت کرد که عدد پی یک عدد جبری نیست و نمیتواند ریشه یک معادله جبری باشد که ضرایب آن گویا هستند. (همانند عدد (e))کشف گنگ بودن عدد پی، به سالها تلاش ریاضیدانان برای تربیع دایره پایان داد.(سایت ویکی پدیا)
[27] باوجود آنکه همه ریاضیدانان میدانند که عدد پی گنگ میباشد و هرگز نمیتوان آن را بهطور دقیق محاسبه کرد اما ارائه فرمولها و مدلهای محاسبه عدد پی هموار برای آنها از جذابیت زیادی برخوردار بودهاست. بسیاری از آنها تمام عمر خود را صرف محاسبه ارقام این عدد زیبا نمودند اما آنها هرگز نتوانستند تا قبل از ساخت کامپیوتر این عدد را بیش از ۱۰۰۰ رقم اعشار محاسبه نمایند. امروزه مقدار عدد پی با استفاده از پیشرفتهترین رایانهها تا میلیونها رقم محاسبه شدهاست؛ و تعداد این ارقام هنوز در حال افزایش است.
اولین محاسبه کامپیوتری در سال ۱۹۴۹ انجام گرفت و این عدد را تا ۲۰۰۰ رقم محاسبه نمود و در اواخر سال ۱۹۹۹ یکی از سوپر کامپیوترهای دانشگاه توکیو این عدد را تا ۲۰۶٬۱۵۸٬۴۳۰٬۰۰۰ رقم اعشار محاسبه نمود. (سایت ویکی پدیا)
آخرین رقم اعشار محاسبه شده، به عدد ۳۱ تریلیون رسیده است.
[28] سؤال یکی از دوستان حاضر در جلسه درس
[29] سئل أمير المؤمنين صلوات الله عليه عن قول الله عز و جل: و كذلك نري إبراهيم ملكوت السماوات و الأرض قال الأصبغ بن نباتة: كنت جالسا بين يديه مطرقا إلى الأرض، فرفع يده إلى فوق ثم قال لي صلى الله عليه: ارفع رأسك فطرقت رأسي، فرفعت رأسي، فرأيت السقف قد انفرج و رأيت نورا ساطعا إلى تحت العرش، فحار بصري فرددته، ثم قال لي صلى الله عليه: يا ابن نباتة، فرأى إبراهيم ملكوت السماوات و الأرض هكذا، ثم قال صلى الله عليه: أطرق رأسك فطرقت رأسي ثم قال: ارفع رأسك، فرفعت رأسي و إذا السقف بحاله.ثم أخذ بيدي فقام و أخرجني من البيت الذي كنا فيه فأدخلني ببيت آخر و خلع ثيابا كانت عليه و لبس ثيابا غيرها، ثم قال: لا تفتح عينك، فلبثت ساعة ثم قال عليه السلام: تدري أين أنت؟ قلت: لا يا مولاي، قال صلى الله عليه: أنت في الظلمة التي سلكها ذو القرنين.فقلت له: جعلت فداك، أ تأذن لي حتى أفتح عيني؟فقال عليه السلام لي: افتح فإنك لا ترى شيئا، ففتحت عيني فإذا أنا في ظلمة لا أبصر فيها موضع قدمي، ثم سار قليلا و وقف و قال: أ تدري أين أنت؟ قلت: لا يا مولاي، قال عليه السلام: أنت واقفعلى عين الحياة التي شرب منها الخضر عليه السلام، و سرنا قليلا إلى عالم آخر فسلكنا فيها فرأيتها كهيئة عالمنا هذا في نباته و ساكنه و أهله، ثم خرجنا إلى عالم ثان حتى وردنا على خمس عوالم ثم قال صلوات الله عليه: هذه ملكوت الأرض كما ترى و هي ثمانية عشر ألف عالم، كل عالم كهيئة ما رأيت.ثم أخذ بيدي فإذا نحن بالبيت الذي خرجنا منه، و نزع تلك الثياب و لبس ثيابه التي كانت عليه، و عدنا إلى مجلسنا، فقلت له: جعلت فداك، كم مضى من النهار؟فقال: ثلاث ساعات (المناقب (للعلوي) / الكتاب العتيق، ص: 8۴-85)
[30] بعضى از خواص براى عالم مثال مطالبى بيان داشتهاند كه براى اكثر مردم قابل قبول نيست، اينان براى گفتههاى خود از اخبار و رواياتى كه در حالات كاملين و صفات آنها رسيده استشهاد نمودهاند از جمله اين فرمايش معصوم كه مىفرمايد: كلنا محمد. همۀ ما محمد هستيم و يا كلنا واحد. همۀ ما يكى هستيم، يا آن روايت كه مىگويد بعضى از نهرهاى بهشتى مشروباتى دارد كه طعم هر مطعوم و مشروبى در آن هست، اينان مىگويند اين بدان خاطر است كه هر موجودى از موجودات آن عالم در بردارندۀ همۀ خصوصيات موجودات ديگر آن عالم نيز هست، و لذا انسان در هر لحظهاى جميع لذاتى كه در همۀ موجودات آن عالم وجود دارد با طعم مخصوص، و لذت خاص آنها، در هريك از آن موجودات مىيابد بدون اينكه خصوصيتى از يكى از آنها از بين برود(اسرار الصلوه،١٣٠)
[31] قال الإمام أبو محمد العسكري (عليه السلام): …فقال تعالى: و لا تقربا هذه الشجرة شجرة العلم، فإنها لمحمد و آله خاصة دون غيرهم، و لا يتناول منها بأمر الله إلا هم، و منها ما كان يتناوله النبي (صلى الله عليه و آله) و علي و فاطمة و الحسن و الحسين (عليهم السلام) بعد إطعامهم اليتيم و المسكين و الأسير، حتى لم يحسوا بعد بجوع و لا عطش و لا تعب و لا نصب.و هي شجرة تميزت بين أشجار الجنة؛ إن سائر أشجار الجنة كان كل نوع منها يحمل نوعا من الثمار و المأكول، و كانت هذه الشجرة و جنسها تحمل البر و العنب و التين و العنابو سائر أنواع الثمار و الفواكه و الأطعمة، فلذلك اختلف الحاكون لذكرالشجرة، فقال بعضهم: هي برة، و قال آخرون: هي عنبة، و قال آخرون:هي تينة، و قال آخرون: هي عنابة. (البرهان في تفسير القرآن، ج1، ص: 178)
در کتاب الثاقب فی المناقب ابن حمزه طوسی نیز چنین آمده است: فبينا نحن وقوف، إذ نحن بغمامة قد أظلتنا ببرق و رعد حتى قربت منا، فألقت بين يدي رسول الله (ص) سفرة عليها رمان، لم تر العيون مثلها، على كل رمانة ثلاثة أقشار: قشر من اللؤلؤ، و قشر من الفضة، و قشر من الذهب.فقال (ص) لي: قل: بسم الله و كل يا علي، هذا أطيب من سفرتك. و كشفنا عن الرمان، فإذا فيه ثلاثة ألوان من الحب: حب كالياقوت الأحمر، و حب كاللؤلؤ الأبيض، و حب كالزمرد الأخضر، فيه طعم كل شيء من اللذة (الثاقب في المناقب، ص:۵٨- 59)
در کافی شریف نیز در وصف رسول مکرم اسلام چنین آمده است:له حوض أكبر من بكة إلى مطلع الشمس من رحيق مختوم فيه آنية مثل نجوم السماء و أكواب مثل مدر الأرض عذب فيه من كل شراب و طعم كل ثمار في الجنة (الكافي (ط – الإسلامية) ؛ ج8 ؛ ص139)
[32] بحث از علامت جمع و ابعاد مختلف آن در مقاله«مثال دقیق، سؤال روان؛ ابزاری برای ارائه مجردات به همگان» قابل مشاهده است.
در دنیای کامپیوتر دو نوع گرافیک برای عکس ها داریم : یکی Raster و دیگری Vector .
درRaster Graphics که به آن گرافیک شطرنجی هم گفته می شود ، تصویر ها به صورت پیکسلی هستند ، طبیعتا هر کدام از این پیکسل ها رنگ خاص خودشان را دارند و جداگانه ذخیره میشوند . همه ی فرمت های bmp، jpg ، و gif از این دسته هستند . ویژگی این مدل تصاویر این است که با بزرگ تر شدنشان، کیفیتشان کمتر میشود.
اما در Vector Graphics که به آن گرافیک بُرداری میگویند یک تصویر، مجموعه ای از نقطه ها ، خط ها ، منحنی ها و چندضلعی ها هست. این نوع گرافیک با مختصات ریاضی سروکار دارد. تصور کنید یک محور x و y ترسیم شده و هرکدام از این بردار ها با متوجه به مختصاتی که دارند ترسیم شدند و سرجای خودشان قرار گرفتند ( منظور از بردار صرفا یک خط راست نیست ). در این روش، به مرورگر دستور میدهیم در فلان نقطه، فلان بردار را ترسیم کن . در این مدل از تصاویر، کیفیت به اندازه وابسته نیست و به طور کلی مستقل از رزولوشن است .
اس وی جی مخفف عبارت Scalable Vector Graphic به معنای نگارهسازی بُرداری مقیاسپذیراست.نمونه یک تصویر SVG را در ادامه مشاهده می کنید.تصویر سمت چپ،نمونه دستورِ داده شده به رایانه و تصویر سمت راست،خروجی دستور به صورت تصویر است.(سایت ویرگول،مقاله اس وی جی چیه و چکار میکنه؟)

به صورت ساده میتوان بیان کرد که دامنه یک تابع، شامل تمام مقادیری است که به عنوان ورودی به تابع داده میشوند و برد تابع نیز مجموعه مقادیر خروجی از تابع را در بر میگیرد.
اما مهمترین نکتهای که باید به آن توجه کنید این است که دامنه و برد، دو مفهوم اساسی در تعریف توابع هستند و با تغییر آنها تعریف تابع نیز تغییر میکند. در ادامه این مطلب از مجله فرادرس، این موضوع به صورت دقیق مورد بررسی قرار میگیرد و تعریف جامعی از دامنه، برد و همدامنه ارائه میشود.
همانطور که میدانید، یک تابع روی مجموعهای از ورودیها عمل میکند و مجموعهای از خروجیها را تولید میکند. بنابراین میتوان بیان کرد که هر تابع از یک سری ورودی و خروجی تشکیل شده است. برای آنکه مفهوم این موضوع را به صورت دقیق متوجه شوید، به مثال زیر توجه کنید.
مثال
درختی که در شکل زیر نشان داده شده است هر سال به اندازه ۲۰ سانتی متر رشد میکند.
بنابراین میتوان بیان کرد که ارتفاع درخت به میزان سن آن با استفاده از تابع h مرتبط است. این تابع را میتوان به شکل زیر نمایش داد.
![]()
بنابراین در صورتی که سن درخت برابر با 10 سال باشد، ارتفاع آن مطابق با رابطه زیر، برابر با 200 سانتی متر خواهد بود.
![]()
رابطه فوق را میتوان اینگونه بیان کرد که تابع h، عدد 10 را به 200 تبدیل کرده است. بنابراین عدد 10 ورودی این تابع و 200 خروجی آن را نشان میدهد. این موضوع با استفاده از رابطه زیر نیز به خوبی نشان داده شده است.
![]()
ورودی و خروجی یک تابع
نکته بسیار مهمی که باید به آن توجه کنید این است که، تمامی مقادیر و اعداد را نمیتوان به عنوان ورودی به تابع معرفی کرد و اگر به تابع ورودی اشتباه بدهیم، ممکن است که تابع عمل نکند و هیچ خروجی را به ما تحویل ندهد.
دانستن اطلاعات کلی درمورد خروجیهای تابع نیز امر بسیار مهمی است. برای مثال اگر بدانیم که این تابع تنها مقادیر مثبت را به عنوان خروجی به ما تحویل میدهد، درک مسئله برای ما بسیار سادهتر خواهد بود.
علاوه بر موارد ذکر شده، میتوان بیان کرد که یک تابع، روی مجموعههای مشخصی عمل میکند. در ادامه برخی از این مجموعهها را مورد مطالعه قرار میدهیم.
به عنوان مثال اول، مجموعه تمام اعداد زوج (مثبت و منفی) را میتوان با استفاده از مجموعه اعداد زیر نمایش داد.
![]()
مشابه مثال بالا میتوان مجموعه اعداد صحیح فرد را نیز به شکل زیر نمایش داد.
![]()
در ادامه مجموعهای شامل تمام اعداد اول را مورد بررسی قرار میدهیم. توجه کنید که عدد اول، یک عدد طبیعی بزرگتر از یک است که به هیچ عددی به غیر از یک و خود آن عدد، بخش پذیر نیست. مجموعه این اعداد در رابطه زیر نشان داده شده است.
![]()
علاوه بر موارد ذکر شده، مجموعهها را میتوان به اعداد طبیعی، صحیح و گویا نیز محدود کرد. به غیر از مجموعههای کلی که در بالا اشاره شد، امکان دارد مجموعههای دلخواهی نیز در توابع به عنوان ورودی یا خروجی تعریف شوند. برای مثال ممکن است ورودی یک تابع تنها شامل اعداد مثبت کوچکتر از ۱۰ و مضرب ۳ باشد. این مجموعه دلخواه را به شکل زیر نمایش میدهند.
![]()
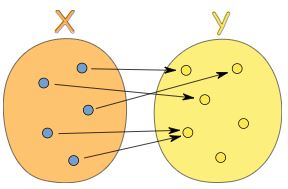
به صورت کلی میتوان بیان کرد که یک تابع، هرکدام از اعضای یک مجموعه را دقیقا به یکی از اعضای مجموعه دیگر مرتبط میکند. توجه کنید که ممکن است دو مقدار از مجموعه اول (دامنه) به یک مقدار از مجموعه دوم (برد) منتقل شوند.
نکته مهم دیگر این است که اگر یک مقدار از مجموعه اول (دامنه) به دو مقدار از مجموعه دوم (برد)، مرتبط شود، با تعرف تابع در تضاد است و این عملگر را نمیتوان تابع نامید. تعریف تابع و مجموعه دامنه و برد در شکل زیر به خوبی نشان داده شده است.
دامنه و برد چیست
دامنه یک تابع، مجموعهای است که به عنوان ورودی تابع در نظر گرفته میشود و برد تابع، مجموعهای است که تمامی خروجیهای تابع را در بر میگیرد.
مجموعه دیگری نیز تحت عنوان همدامنه در تعریف تابع حضور دارد. همدامنه شامل مجموعهای از اعداد است که خروجی تابع میتواند جزئی از آنها باشد. همدامنه را دامنه مشترک نیز مینامند. برای مشخص شدن مفهوم این تعاریف به مثال زیر توجه کنید.
مثال
تابعی با رابطه زیر را در نظر بگیرید.
![]()
این تابع مانند شکل زیر بین مجموعههای A و B عمل میکند و هر عضو مجموعه A را به یک عضو مجموعه B مرتبط میسازد.
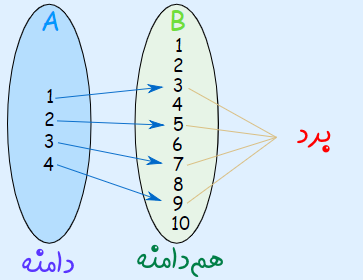
بنابراین مجموعه A، دامنه تابع را نمایش میدهد و مجموعه B، همدامنه را مشخص میکند. توجه کنید که همدامنه را معمولا صورت مسئله تعیین میکند و برد، زیر مجموعهای از این همدامنه است.
در این مثال، برد تابع، مجموعهای است که اعداد 3، 5، 7 و 9 را شامل میشود. برد این تابع زیر مجموعهای از همدامنه (مجموعه B) است. این سه مجموعه یعنی دامنه، همدامنه و برد را میتوان به کمک مجموعههای زیر هم نمایش داد.
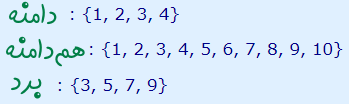
اجزای مختلف یک تابع
در تعریف تابع، دامنه و برد نشان دادیم که آنچه که از تابع بیرون میآید (برد تابع) وابستگی مستقیم به ورودی تابع (دامنه تابع) دارد. بنابراین میتوان بیان کرد که یکی از مهمترین بخشهای تابع، دامنه آن است و تغییر دامنه باعث تغییر خروجی تابع و ویژگیهای مختلف آن تابع میشود.
برای مشخص شدن مفهوم این قضیه به مثال زیر توجه کنید.
مثال
تابع سادهای را که رابطه آن به فرم f(x)=x2 است را در نظر بگیرید. دامنه این تابع یعنی آنچه به عنوان ورودی به تابع داده میشود را میتوانیم مجموعهای شامل اعداد طبیعی به فرم {1,2,3,…} تعریف کنیم. با استفاده از این دامنه و رابطه تابع، برد تابع به فرم مجموعه زیر در میآید.
{1,4,9,…}
این تابع با استفاده از دامنه و بردی که در بالا تعریف شد، به صورت زیر مشخص میشود.
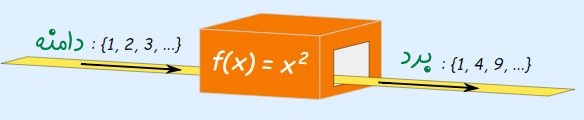
حال تابع دیگری که رابطه مشابهی با تابع قبلی دارد را در نظر بگیرید. ابن تابع را با حرف g و با استفاده از رابطه g(x)=x2 میتوان مشخص کرد. دامنه این تابع را به صورت مجموعه تمام اعداد صحیح به فرم زیر در نظر بگیرید.
![]()
در این شرایط، برد تابع به شکل زیر در میآید.
![]()
توجه کنید که برد تابع جدید نسبت به حالت قبل یک عدد صفر (0) بیشتر دارد. این تابع، دامنه و برد آن را میتوان به شکل زیر نمایش داد.
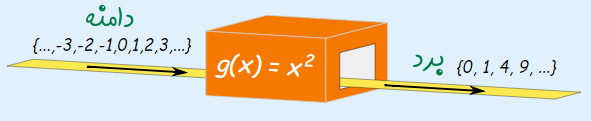
همانطور که مشاهده میشود، هر دو تابع مجذور ورودی را به عنوان خروجی تحویل میدهند ولی از آنجایی که این دو تابع ورودی و دامنه متفاوتی دارند، خروجی و برد آنها نیز متفاوت خواهد بود.
توجه کنید که خواص این دو تابع نیز متفاوت است. در حالت اول، تابع f، به صورت یک به یک است و به ازای هر ورودی یک خروجی را تولید میکند. این در حالی است که تابع g یک به یک نیست و به ازای دو ورودی مختلف، یک جواب یکسان را تولید میکند. این موضوع در دو رابطه زیر نشان داده شده است.
![]()
![]() بنابراین با توجه به مثال و توضیحات بالا، میتوان نتیجه گرفت که یکی از بخشهای اساسی تابع، دامنه آن است. انواع مختلف دامنه میتواند ویژگیهای گوناگون تابع را تحت تاثیر خود قرار دهد. (سایت فرادرس، مقاله دامنه و برد تابع)
بنابراین با توجه به مثال و توضیحات بالا، میتوان نتیجه گرفت که یکی از بخشهای اساسی تابع، دامنه آن است. انواع مختلف دامنه میتواند ویژگیهای گوناگون تابع را تحت تاثیر خود قرار دهد. (سایت فرادرس، مقاله دامنه و برد تابع)
[35] ایده اصلی برای بهرهگیری از رابطه بین متغیرها و تعریف تابع در قرن ۱۷ میلادی شکل گرفت و تحلیل خصوصیات توابع، باعث بوجود آمدن شاخه «حسابان» (Calculus) در ریاضیات شد. در آن زمان فقط «تابع حقیقی» (Real Function) یا توابع با متغیرهای «حقیقی مقدار» (Real Valued) مورد بحث واقع شده و فرض بر این بود که همه توابع «هموار» (Smooth) هستند. موضوعات مربوط به تابع و نگاشت همچنین دامنه و همدامنه، بعدها در قرن ۱۹ توسط ریاضیدانان، مورد پژوهش واقع شد. بنا به اهمیت توابع و نقش آنها در ریاضیات پایه و عمومی، این نوشتار از مجله فرادرس را به این گونه توابع اختصاص دادهایم. البته در این بین تفاوت تابع حقیقی و نگاشت (Map) نیز بیان شده و خصوصیات هر یک مورد بحث قرار میگیرد.
تعریف تابع و نگاشت در ریاضیات
به طور شهودی، میتوان تابع را یک فرآیند یا «عملگر دو دویی» (Binary Operation) در نظر گرفت که به واسطه آن هر عنصری از یک مجموعه به یک عنصر به مجموعه دیگر مرتبط میشود. البته نحوه ارتباط در اینجا دارای شرایطی است که در ادامه به آن خواهیم پرداخت.
به طور رسمی تابع f از مجموعه X به مجموعه Y به صورت یک مجموعه است که شامل زوجهای مرتبی مثل (x,y) بوده که عنصر اول آن از مجموعه X گرفته شده و مولفه دوم آن نیز متعلق به مجموعه Y است. در این بین شرطی وجود دارد که طی آن هر عنصری از X نباید بیش از یک بار در تابع یا مجموعه زوجهای مرتب، به کار رفته باشد. به بیان دیگر نباید به ازاء یک مقدار از مجموعه X دو مقدار در تابع یا مجموعه Y پیدا شود.
نکته: اگر چنین اتفاقی بیافتد، مجموعه زوجهای مرتب را یک «رابطه» (Relation) مینامند. پس هر تابع یک رابطه است ولی هر رابطه، یک تابع نیست.
نگاشت در ریاضیات
اغلب هر تابع را یک «نگاشت» (Map) در نظر میگیرند ولی بعضی ریاضیدانان، برای مفهوم نگاشت و تابع، تمایز قائل میشوند. برای مثال «سرژ لانگ» (Serge Lang)، ریاضیدان آمریکایی-فرانسوی، تابع را برای نگاشتهایی که همدامنه آن زیرمجموعهای از اعداد حقیقی یا مختلط است به کار میبرد و معتقد است که نگاشت حالت کلیتری از تابع را شامل میشود.
از طرفی، اغلب منظور از نگاشت همان «همریختی» (Homomorphism) است. مثلا برای نشان دادن یک گروه همریخت از G به H از اصطلاح نگاشت خطی یا نگاشت از G به H استفاده میکنند. گاهی هم زمانی یک تابع را نگاشت مینامند که همدامنه آن دقیقا منطبق با مجموعه مقادیر تابع باشد. به H از اصطلاح نگاشت خطی یا نگاشت از G به H استفاده میکنند. گاهی هم زمانی یک تابع را نگاشت مینامند که همدامنه آن دقیقا منطبق با مجموعه مقادیر تابع باشد.(سایت فرادرس، مقاله تابع حقیقی و نگاشت در ریاضیات)
[36] یک معقول منفصل نه مثال منفصل
دیدگاهتان را بنویسید